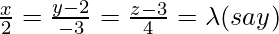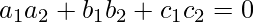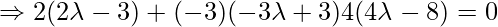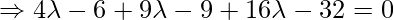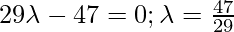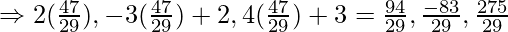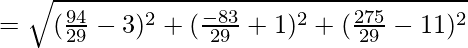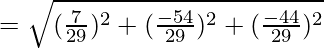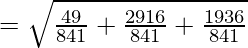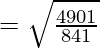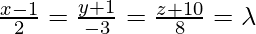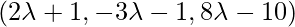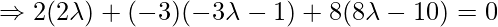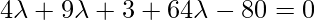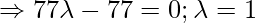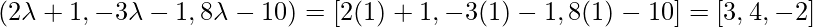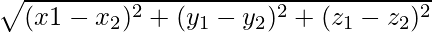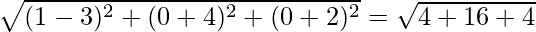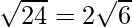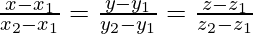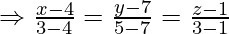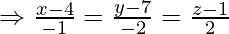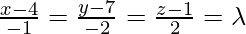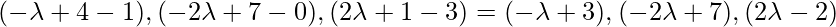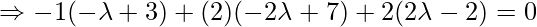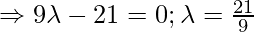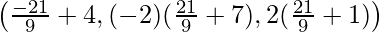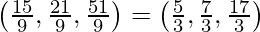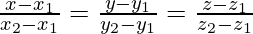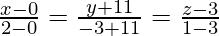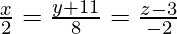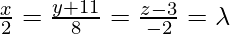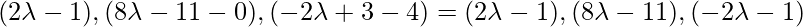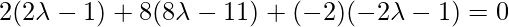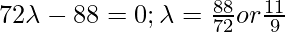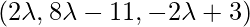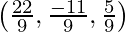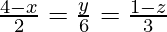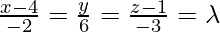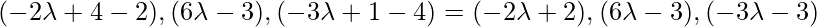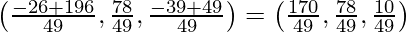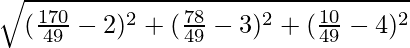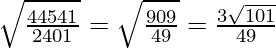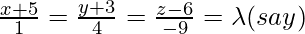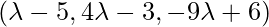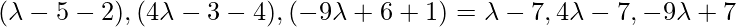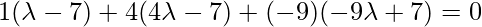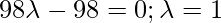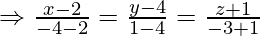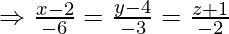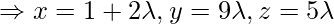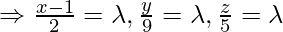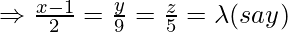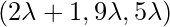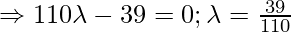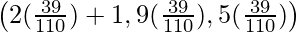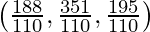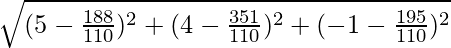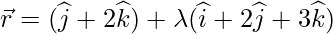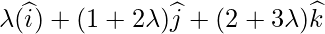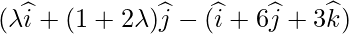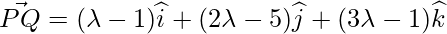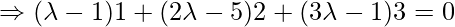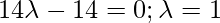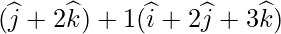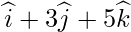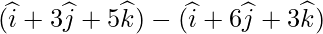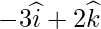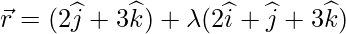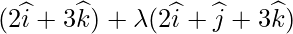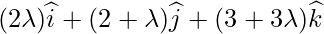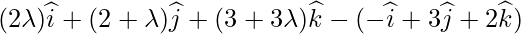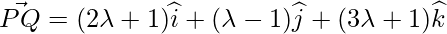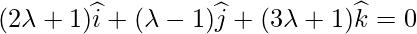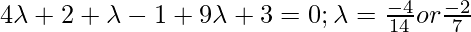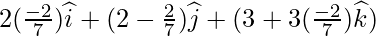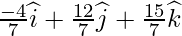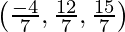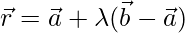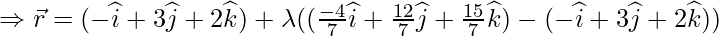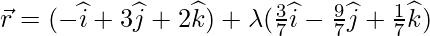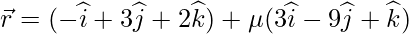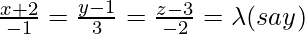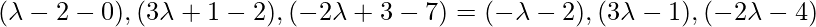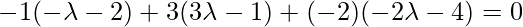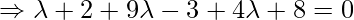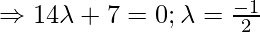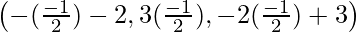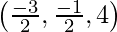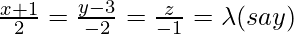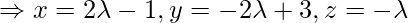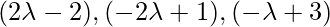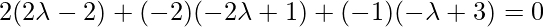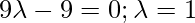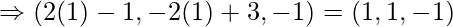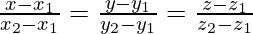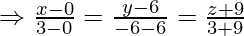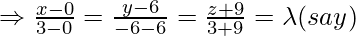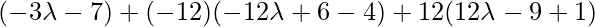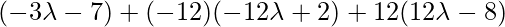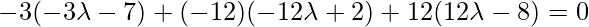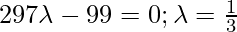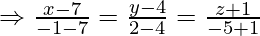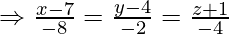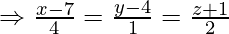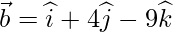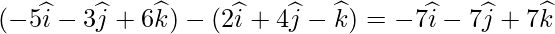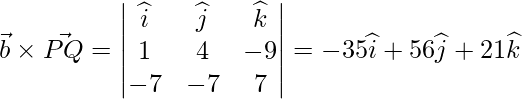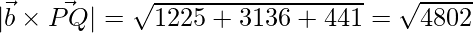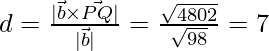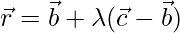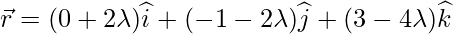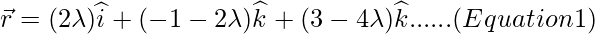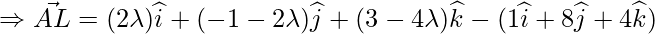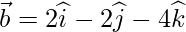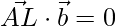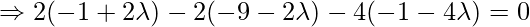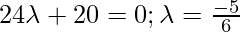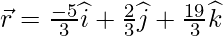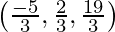Класс 12 Решения Р. Д. Шармы - Глава 28 Прямая линия в космосе - Упражнение 28.4
Вопрос 1. Найдите перпендикулярное расстояние точки (3, -1, 11) от прямой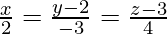 
Решение:
Let the foot of the perpendicular drawn from P (3, -1, 11) to the line
is Q, so we have to find length of PQ is general point on the line
Coordinate of Q =
, direction ratios of the given line = 2,-3,4. Since PQ is the perpendicular to the given line interface.
So, the coordinates of Q are:
Distance between P and Q is given as:
So, the required distance is
units
Вопрос 2. Найдите перпендикулярное расстояние точки (1,0,0) от прямой. 
. Также найдите координаты основания перпендикуляра и уравнение перпендикуляра.
Решение:
Let us consider the foot of the perpendicular drawn from P (1,0,0) to the line
is Q. So let us find the length of PQ i.e.
Coordinate of Q =
The direction ratios of the given line:
So the Coordinates of Q are as follows:
Distance between P and Q is given by:
PQ =
PQ =
PQ =
Hence, the foot of the perpendicular = (3,-4,-2);
Length of the perpendicular =
units.
Вопрос 3. Найдите основание перпендикуляра, проведенного из точки A (1,0,3) к стыку точек B (4,7,1) и C (3,5,3).
Решение:
Let us consider, the foot of the perpendicular drawn from A(1,0,3) to the line joining
Points B(4,7,1) and C(3,5,3) be D. The equation of the line passing through
points B(4,7,1) and C(3,5,3) is
Let
So, the direction ratio of AD is
Line AD is the perepndicular to BC so,
Hence, coordinates of D are:
=
Вопрос 4. A (1,0,4), B (0, -11,3), C (2, -3,1) - три точки, а D - основание перпендикуляра из A на BC. Найдите координаты D.
Решение:
Given: D is the perpendicular from A(1,0,4) on BC. So,
Equation of line passing through BC is:
Coordinates of D = (
)
Direction ratios of AD is
Line AD is perpendicular to BS so,
So, coordinates of D are =
=
Вопрос 5. Найдите основание перпендикуляра от точки (2,3,4) до прямой.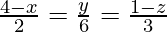 
. Также найдите перпендикулярное расстояние от данной точки до линии.
Решение:
Let us consider that The foot of the perpendicular drawn from P(2,3,4) to the line
.
Equation of the line is
Let
Coordinates of Q =
So, PQ is perpendicular to the given line,
Coordinates of Q =
=
=
Distance between P and Q is given by: PQ =
=
=
Hence, perpendicular distance from (2,3,4) to the given line is
units.
Вопрос 6. Найдите уравнение перпендикуляра, проведенного из точки P (2,4, -1) к прямой.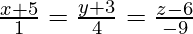 
. Также запишите координаты подошвы перпендикуляра из P.
Решение:
Let
Given line is
Coordinate of Q (General point on the line) =
Direction ratios of PQ are:
As line PQ is perpendicular to the given line, so:
Therefore, coordinates of foot of perpendicular = {-4, 1, -3}
So equation of the perpendicular PQ is :
Вопрос 7. Найдите длину перпендикуляра, проведенного из точки (5,4, -1) к прямой.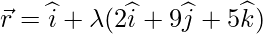 
Решение:
Let the foot of the perpendicular drawn from P(5,4,-1) to the given line is Q, so given equation of line is:
Equating the coefficients of
Coordinate of Q =
Direction ratios of line PQ are:
As line PQ is perpendicular to the given line, so:
Coordinate of Q = {
}
=
=
Length of perpendicular = PQ =
=
PQ =
Вопрос 8. Найдите основание перпендикуляра, проведенного из точки. 
к линии 
. Также найдите длину перпендикуляра.
Решение:
Let position vector of foot of perpendicular drawn from p
on
be Q
. So, Q is on the line
So, position vector of Q =
is the position vector of Q – position vecor of p =
Here, PQ vector is perpendicular to the given line. So,
Position vector of Q = {
}
=
Foot of the perpendicular =
= Position vector of Q – Position vector of P
=
=
=
units
Вопрос 9. Найдите уравнение перпендикуляра drwan от точки P (-1,3,2) до прямой 
. Также найдите координаты основания перпендикуляра от P.
Решение:
Let Q be the perpendicular drawn from P {
} on the
vector
Let the position vector of Q be :
:
As PQ vector is perpendicular to the given line,
Position Vector of Q =
is
Coordinates of foot of the perpendicular:
Equation of PQ is:
Вопрос 10. Найдите основание перпендикуляра из (0,2,7) на прямой.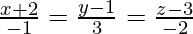 
Решение:
Let the foot of the perpendicular drawn from (0,2,7) to the line
be Q.
Given equation of the line is
Coordinate of Q = {
}
Direction Ratios of PQ are
Since, PQ is perpendicular to the given line, so
Foot of the perpendicular = {
}
=
Вопрос 11. Найдите основание перпендикуляра от (1,2, -3) до прямой.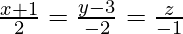 
Решение:
Let the foot of perpendicular from P (1,2,-3) to the line
be Q.
Given the equation of line is
Coordinates of Q are {
}
Direction Ratios of PQ are:
=
Let PQ be the perpendicular to th egiven line, so
Coordinate of the perpendicular:
Вопрос 12. Найдите уравнение прямой, проходящей через точки A (0,6, -9) и B (-3, 6, 3). Если D - основание перпендикуляра, проведенного из точки C (7,4, -1) на прямой AB, то найдите координаты точки D и уравнение прямой CD.
Решение:
Equation of line AB is
Coordinate of point D = {
}
Direction ratios of CD =
=
As line CD is perpendicular to the line AB, so
Coordinate of D = {
= {
}
= (-1,2,-5)
Equation of CD is
Вопрос 13. Найдите расстояние точки (2,4, -1) от линии.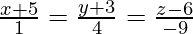 
Решение:
Let P = (2,4,-1)
In order to find the distance we need to find a point Q on the line. We see that line is passing through
the point Q(-5,-3,6). So, let’s take this point as the required point.
The line is also parallel to the vector
Now,
Therefore,
Вопрос 14. Найдите координаты основания перпендикуляра, проведенного из точки A (1,8,4) к прямой, соединяющей точки B (0, -1,3) и C (2, -3, -1).
Решение:
Let L be the foot of the perpendicular drawn from A(1,8,4) on the line joining the points B(0,-1,3) and C(2,-3,-1).
Equation of the line passing through the points B and C is given by
Let position vector of L be,
Then,
= Position vector of L – Position vector of A
Since, AL vector is perpendicular to the given line
which is parallel to
Therefore,
Putting value of lambda in Equation 1, we get:
So, coordinates of foot of the perpendicular are
