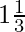Как сложить смешанные дроби с целыми числами?
Прежде чем узнать, как мы можем складывать смешанные дроби с целыми числами, мы должны знать, что такое дроби и целые числа. Система счисления является основной концепцией целых чисел и смешанных дробей. Если у нас есть ясность относительно системы счисления, мы можем легко решить концепцию сложения смешанных дробей с целыми числами. В системе счисления есть такие понятия, как целые числа, натуральные числа, целые числа и действительные числа.
Система счисления представляет собой комбинацию натуральных чисел, целых чисел, целых чисел и действительных чисел.
Натуральные числа: Натуральные числа — это числа, которые могут считать числа. Мы также можем сказать, что числа начинаются от 1 до бесконечности без включения 0. Примеры,
Natural numbers={1,2,3,4,5,6,7,8,9,10,11,12,13….}
Целые числа: Целые числа — это числа в союзе натуральных чисел и нуля (0). Целое число — это один из типов системы счисления, в котором ноль входит в число натуральных чисел. Примеры,
Whole numbers= {0,1,2,3,4,5,6,7,8,9,10,11,12,13.15,16,17,18….}
Целые числа: Целочисленная система — это система счисления, в которой отрицательные числа и положительные натуральные числа включены в ноль (0). Целые числа — это числа, представляющие собой объединение отрицательных целых чисел и целых чисел. Примеры,
Integers={…-2,-1,0,1,2…..}
Рациональные числа: Рациональные числа — это числа, имеющие форму r/a, только где a не должно равняться нулю. Рациональные числа также называют конечными числами.
Примеры,
Rational numbers: 0/1, 1/1, 2/1, 3/1,1.9999 etc.
Иррациональные числа: Иррациональные числа — это числа, которые не представлены в виде r/b, где b не должно равняться нулю, а также называются неконечными числами.
Примеры,
Irrational numbers: √2,√3, 0.12356…
Вещественные числа: Вещественные числа являются частью системы счисления, в которой сочетаются как рациональные, так и иррациональные числа.
Дроби: Дроби основаны на числителе и знаменателе. Дроби подобны рациональным числам, представленным как часть целых чисел. Предположим, что прямоугольник разделен на четыре части, так что каждая часть делится на 1/3 и представляет собой 1:3, где 1/3 или 1:3 — дробная часть прямоугольника.
Примеры дробей:
7/8 where 7 is the numerator and 2 is the denominator.
1/4 where 1 is the numerator and 4 is the denominator.
9/3 where 9 is the numerator and 3 is the denominator.
Фракции бывают трех видов. Они есть,
- Правильная дробь: Правильная дробь является одним из видов дроби. Правильная дробь объясняется тем, что числитель должен быть меньше знаменателя.
Примеры правильных дробей: 1/2, 3/5, 6/8…. - Неправильная дробь: Неправильная дробь — это один из видов дроби. Он определяется как числитель, который должен быть больше знаменателя.
Примеры неправильных дробей: 8/6, 9/7, 3/2 и так далее. - Смешанная дробь: Смешанная дробь представляет собой объединение дробной части (содержит как правильные, так и неправильные) и натуральных чисел.
Примеры смешанных фракций показаны ниже:
здесь 1 — целое число, 2 — числитель, 3 — знаменатель.
Как преобразовать смешанные дроби в форму p/q?
Step 1: First multiply the whole number with the denominator.
Step 2: Add the numerator and result of multiplication of the whole number with denominator.
Step 3: Result from Step2 should be placed in the numerator part where the denominator is the same as in the mixed fraction. Hence we got the mixed fraction into proper p/q form.
Как преобразовать неправильные дроби в смешанные дроби?
Let’s take 8/6 as an improper fraction
Step 1: First, divide the numerator with denominator 8//6 = 1 as quotient and remainder as 2.
Step 2: Remainder 2 which divides by 6.
Step 3: Remainder should divide with denominator. If there is a cancellation that occurs cancel with the appropriate factor.
Step 4: When we rationalize 2/6 we get 1/3. Combining Step 1 answer and Step 4 we get
Как сложить целое число со смешанной дробью?
- Сначала мы должны преобразовать смешанную дробь в форму p/q.
- Затем преобразуйте эту форму p/q в десятичную форму.
- Затем сложение целого числа с десятичной формой p/q.
Примеры проблем
Задача 1: Решите приведенный ниже вопрос, который имеет форму сложения целых чисел и смешанной дроби?
10 + 
Решение:
To solve this problem we have to solve mixed fractions first.
Solving mixed fraction:
Step 1: Multiply whole number 10 with denominator 3 as shown in diagram = 10×3=30.
Step 2: Adding numerator 2 with result in Step1 = 2+30=32.
Step 3: In p/q form numerator p=32 and denominator q=3. Therefore 32/3=10.7 is the proper p/q form.
After converting the mixed fraction part to the proper p/q form. Add the whole number with a mixed fraction.
Add 10 with 32/3=10.7 we get 20.7 as a result of the addition.
Therefore by solving the above problem we will get the result of 20.7 which is also represented in p/q=207/10.
Задача 2: Решите приведенный ниже вопрос, который имеет форму сложения целых чисел и смешанной дроби?
20 + 
Решение:
To solve this problem we have to solve mixed fractions first.
Solving mixed fraction:
Step 1: Multiply whole number 1 with denominator 3 as shown in diagram = 1×3=3.
Step 2: Adding numerator 2 with result in Step1 = 2+3=5.
Step 3: In P/q form numerator p=5and denominator q=3. Therefore 5/3=1.7 is the proper p/q form.
After converting the mixed fraction part to the proper p/q form. Add the whole number with a mixed fraction.
Add 20 with 5/3=1.7 we get 21.7 as a result of the addition.
Therefore by solving the above problem we will get the result of 21.7 which is also denoted as p/q form 217/10.
Задача 3: Решите вопрос ниже, который имеет форму сложения целых чисел и смешанной дроби?
13 + 
Решение:
To solve this problem we have to solve mixed fractions first.
Solving mixed fraction:
Step 1: Multiply whole number 2 with denominator 3 as shown in diagram = 2×3=6.
Step 2: Adding numerator 1 with result in Step1 = 1+6=7.
Step 3: In p/q form numerator p=7and denominator q=3. Therefore 7/3=2.33 is the proper p/q form.
After converting the mixed fraction part to the proper p/q form. Add the whole number with a mixed fraction.
Add 13 with 7/3=2.33 we get 15.33as a result of the addition.
Therefore by solving the above problem we will get the result of 15.33 which is also denoted as p/q form 153.3/10.
Задача 4: Решите приведенный ниже вопрос, который имеет форму сложения целых чисел и смешанной дроби?
16 +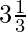 
Решение:
To solve this problem we have to solve mixed fractions first.
Solving mixed fraction:
Step 1: Multiply whole number 3 with denominator 3 as shown in diagram = 3×3=9.
Step 2: Adding numerator 1 with result in Step1 = 1+9=10.
Step 3: In p/q form numerator p=10 and denominator q=3. Therefore 10/3=3.33 is the proper p/q form.
After converting the mixed fraction part to the proper p/q form. Add the whole number with a mixed fraction.
Add 16 with 10/3=3.33 we get 19.33as a result of the addition.
Therefore by solving the above problem we will get the result of 19.33 which is also denoted as p/q form 193.3/10.