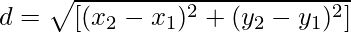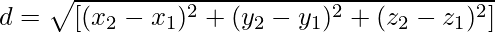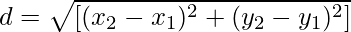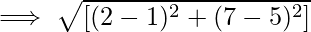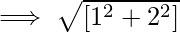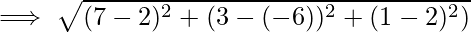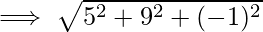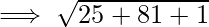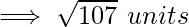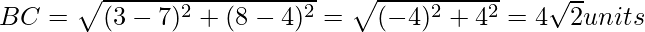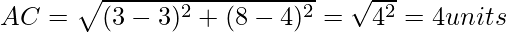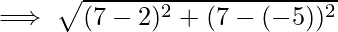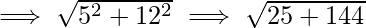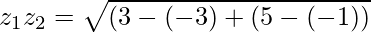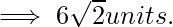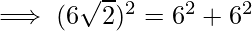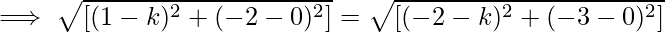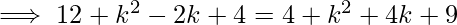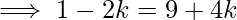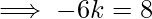Как рассчитать расстояние между двумя точками?

Длина отрезка, соединяющего две точки, определяется как расстояние между ними. Длину отрезка, соединяющего указанные координаты, можно использовать для вычисления расстояния между двумя точками в координатной геометрии. Давайте посмотрим на формулу расчета расстояния между двумя точками на двумерной или трехмерной плоскости.

Каково расстояние между двумя точками?

Расстояние отрезка, соединяющего любые две точки, равно расстоянию между ними. Есть только одна линия, соединяющая две точки. В результате расстояние между двумя точками можно вычислить, определив длину отрезка, соединяющего две точки. Например, если A и B — две точки, а AB = 20 см, это означает, что расстояние между A и B равно 20 см.

Длина отрезка, соединяющего две точки, равна расстоянию между ними (но это НЕ МОЖЕТ быть длиной соединяющей их кривой). Важно отметить, что расстояние между двумя точками всегда положительно.

Формула расстояния между двумя точками

Формула расстояния используется для определения расстояния между двумя точками с использованием предоставленных координат. Мы используем формулу двумерного расстояния или формулу евклидова расстояния для расчета расстояния между любыми двумя точками на двумерной плоскости.

Формула для расстояния между двумя точками

Формула для расстояния d между двумя точками с координатами (x ₁ , y ₁ ) и (x _{2 ,} y ₂ ) выглядит следующим образом:

Это называется формулой расстояния.

Чтобы найти расстояние между двумя точками, заданными в трехмерной плоскости, мы можем применить формулу трехмерного расстояния, заданную как

Вывод формулы для расстояния между двумя точками

Чтобы получить формулу для вычисления расстояния между двумя точками на двумерной плоскости, предположим, что есть две точки с координатами A (x ₁ , y ₁ ) и B (x ₂ , y ₂ ). После этого будем считать, что отрезок, соединяющий A и B, равен AB = d. Теперь нанесем указанные точки на координатную плоскость и соединим их линией.

Далее построим прямоугольный треугольник, используя AB в качестве гипотенузы.

Используя теорему Пифагора,

АВ ² = АС ² + ВС ²

d ² = (x ₂ ​−x ₁ ​) ² + (y ₂ ​−y _{1​ )} ²

Здесь вертикальное расстояние между заданными точками равно | у ₂ – у ₁ |

Расстояние по горизонтали между заданными точками равно | х ₂ – х ₁ |

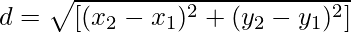(извлечение квадратного корня с обеих сторон)

Таким образом, формула расстояния для нахождения расстояния между двумя точками доказана.

Используя аналогичные шаги и концепцию, мы также можем вывести формулу для нахождения расстояния между двумя точками, заданными в трехмерной плоскости.

Шаги, чтобы найти расстояние между двумя точками

Следующие шаги могут быть использованы для определения расстояния между двумя местами с использованием предоставленных координат:

• Запишите координаты двух заданных точек на координатной плоскости следующим образом: A( _x1 , _y1 ) и B( _x2 , _y2 ).
• Мы можем использовать формулу расстояния, чтобы вычислить расстояние между двумя точками,
• Выразите полученный ответ в единицах.

Note: We can apply the 3D distance formula in case the two points are given in 3D plane,

Примеры проблем

Задача 1: Найдите расстояние между двумя точками с координатами, заданными как A (1,5) и B (2,7).

Решение:

Let (x₁, y₁) be (2,7) and (x₂, y₂) be (1,5).

The distance d between the points : 

The distance between the two points is √5 units.

Задача 2: Найдите расстояние между двумя точками с координатами, заданными как P (2,-6,2) и Q(7, 3, 1).

Решение:

Let (x₁, y₁, z₁) be P (2,-6,2) and (x₂, y₂, z₂) be Q (7,3,1).

The distance d between the points P and Q : 

Задача 3. Докажите, что вершинами прямоугольного треугольника являются точки (3, 4), (7, 4) и (3, 8).

Решение:

Let us say the given points be:

P = (3, 4)

Q = (7, 4)

R = (3, 8)

Now, we will find each vertices of the right-angle triangle by distance formula.

 

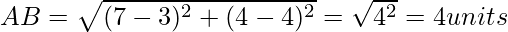
As we know the length of the sided of the right-angled triangle, by Pythagoras Theorem;

AB² + AC² = BC²

4²+4²=(4√2​)²

16+16 = 32⟹32 = 32

This proves that ABC is a right-angle triangle.

Расстояние между двумя точками на комплексной плоскости

Расстояние между двумя точками комплексной плоскости или двумя комплексными числами z ₁ ​=a+ib а z ₂ ​=c+id в комплексной плоскости ⟹1−2k=9+4k представляет собой расстояние между точками (a, b) и (c, d), заданное как

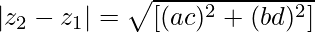
Задача 4: найти расстояние между двумя комплексными числами z ₁ ​= 2−5i и z ₂ ​= 7+7i

Решение:

Here, we have two complex numbers  z₁ = 2-5i and z₂ = 7+7i.

The distance between these complex numbers is equidistance to the two points in the plane, with coordinates, (2,-5) and (7,7).

Thus, distance between the two points is

 

Hence, the distance between two complex numbers z_1=2-5i and z_2=7+7i is 13 units.

Задача 5. Комплексное число ω равно 6 единицам кроме z ₁ = -3 – i и 6 единицам кроме z ₂ = 3 + 5i. Проверьте, является ли треугольник, образованный ω, z ₁ , z ₂ , прямоугольным или нет.

Решение:

There are 3 complex numbers ω, z₁, z₂.

As we know the distance between ω and z₁ is 6 units and distance between ω and z₂ is 6 units.

Given,  ω, z₁ = 6 units

ω, z₂ = 6 units

Now, we will find the distance between z₁ and z₂ by using distance formula.

 

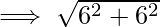
By Pythagoras Theorem, we have;

(z₁​z₂​)²=(ωz₁​​)²+(ωz₂)​²

Hence, we conclude that the given triangle is right-angle triangle.

Задача 6: Найдите точку на оси x, равноудаленную от точек (1, -2) и (-2, -3).

Решение:

We know that any point on the x-axis has an y-coordinate of 0. As a result, we consider the point equidistant from the provided points to be (k,0). i.e., Distance between ( k,0) and (1, -2) = Distance between (k, 0) and (-2, -3).

 

implies   -4k-2k= 9-1

 

Therefore, the required point is (k, 0) =