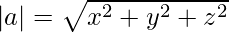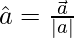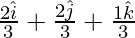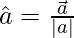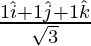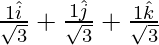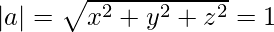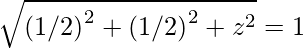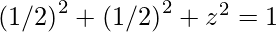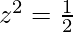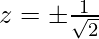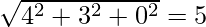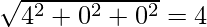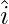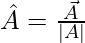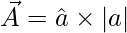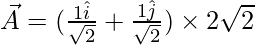Как рассчитать единичный вектор?
Физические величины делятся на два типа: «векторные» и «скалярные». Термин «вектор» относится к физической величине, которая имеет как величину, так и направление. Это физические величины, которые подчиняются треугольному закону сложения векторов. Некоторыми примерами векторных величин являются электрическое поле, смещение, импульс, скорость, сила и ускорение. Все эти величины имеют как величину, так и направление. С другой стороны, «скалярные» величины имеют только величину. Некоторыми примерами скалярных величин являются расстояние, длина, объем, температура и площадь.
Типы векторов
- Равные векторы: векторы, имеющие одинаковую величину и одинаковое направление, называются равными векторами.
- Коллинеарные векторы. Векторы, направленные либо в одном, либо в противоположном направлении друг к другу, называются коллинеарными векторами.
- Параллельные векторы. Параллельные векторы также известны как подобные векторы . Коллинеарные векторы с одинаковыми направлениями называются параллельными векторами. Угол между этими векторами равен нулю.
- Антипараллельные векторы: Антипараллельные векторы также известны как непохожие векторы. Коллинеарные векторы с противоположными направлениями называются антипараллельными векторами. Угол между этими векторами равен 180°.
- Копланарные векторы: все векторы, лежащие в одной плоскости, называются копланарными векторами.
- Нулевые векторы. Вектор с одинаковыми начальной и конечной точками называется нулевым вектором. Его также называют нулевым вектором . Величина такого вектора равна 0, а его направление неопределенно.
Вычисление единичного вектора
Единичный вектор - это вектор величины 1 и с направлением вдоль данного вектора. Он представляет направление данного вектора. Единичный вектор вектора находится путем деления вектора на его модуль. Модуль вектора - это величина вектора.
It is represented by symbol ‘
‘(hat or cap) over a variable as
and is given by,
Where |A| is the modulus of vector A and for a vector
, |A| is given by,
Thus for a vector
Примеры проблем
Проблема 1: Дано 
. Находить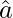 
.
Решение:
Modulus of the vector,
=
= √9
= 3
Unit vector,
=
=
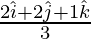
Проблема 2: Является ли вектор заданным 
тоже единичный вектор?
Решение:
Modulus of the vector,
=
= √3
Magnitude of this vector is not 1. Hence, it is not a unit vector.
Задача 3: найти единичный вектор в направлении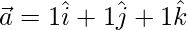 
.
Решение:
Modulus of the vector,
=
Unit vector,
=
=
Проблема 4: Если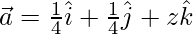 
является единичным вектором, затем найдите значение z.
Решение:
Magnitude of a unit vector is 1, which means:
which means,
Squaring both sides,
Вопрос 5: Найдите единичный вектор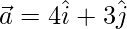 
.
Решение:
Modulus of the vector,
=
Unit vector,
=
=
Вопрос 6: Найдите единичный вектор вдоль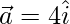 
.
Решение:
Modulus of the vector,
=
Unit vector,
=
=
Вопрос 7: Если единичный вектор вдоль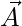 
величины 2√2 составляет 
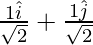. Находить .
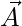Решение:
Unit vector,
Which means
Thus,
