Измерения графика: длина, расстояние, диаметр, эксцентриситет, радиус, центр

Предварительное условие - Основы теории графов - Набор 1, Набор 2
Граф определяется как набор точек, известных как «вершины», а линия, соединяющая эти точки, называется «ребрами». Это набор, состоящий из где V - вершины, а E - ребро.

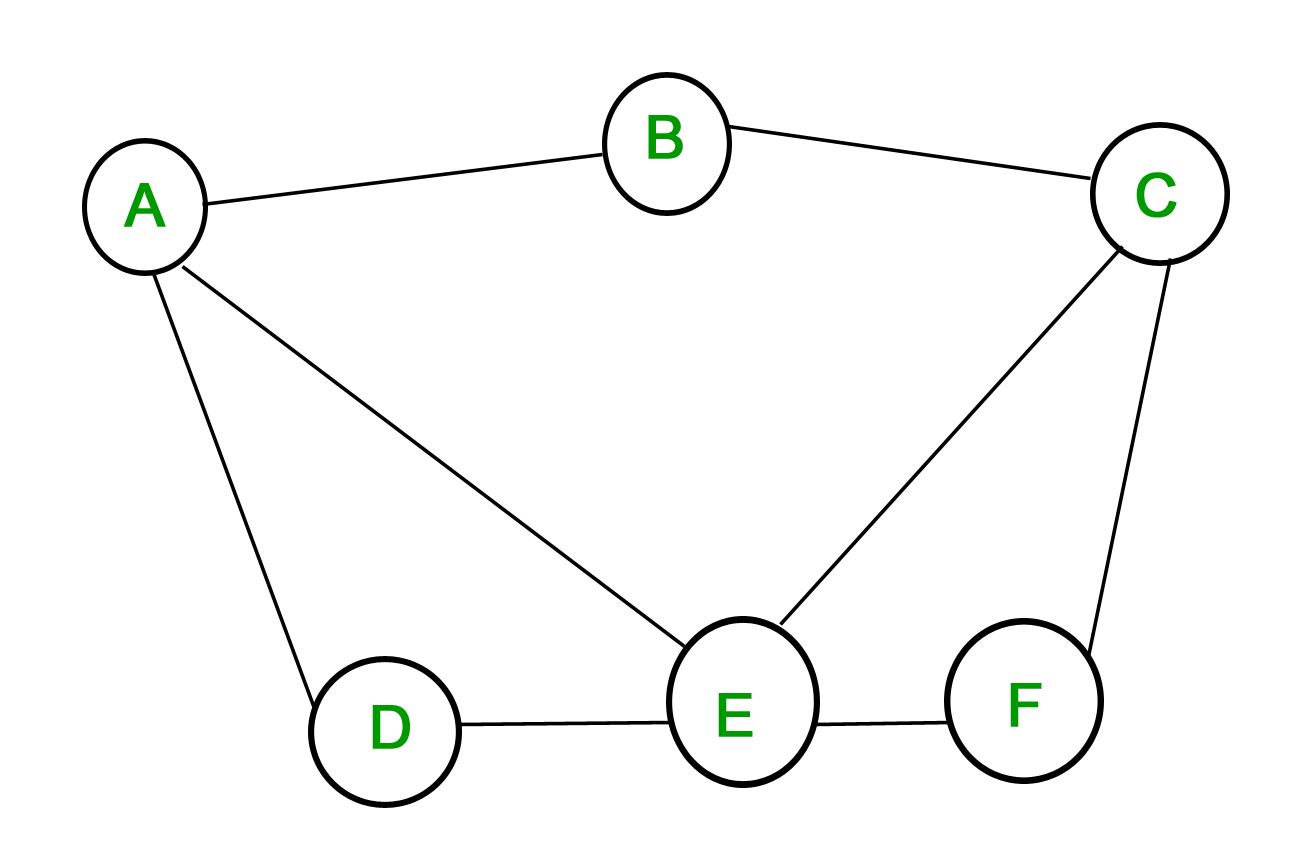
Вершины: {A, B, C, D, E, F}
Края: {{A, B}, {A, D}, {A, E}, {B, C}, {C, E}, {C, F}, {D, E}, {E, F} }

Графические измерения. Доступно несколько методов графических измерений:

1. Длина -
Длина графа определяется как количество ребер, содержащихся в графе.

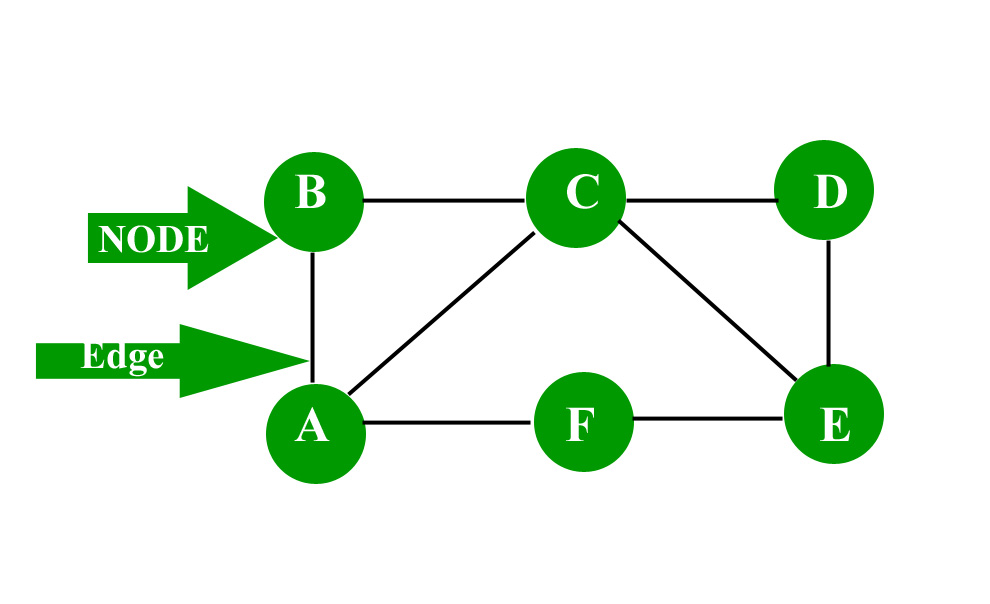
Длина графика: 8
AB, BC, CD, DE, EF, FA, AC, CE

2. Расстояние между двумя вершинами -
Расстояние между двумя вершинами в графе - это количество ребер на кратчайшем или минимальном пути. Это дает доступное минимальное расстояние между двумя краями. Между двумя вершинами может существовать более одного кратчайшего пути.

Кратчайшее расстояние от 1 до 5 равно 2
1 → 2 → 5

3. Диаметр графика -
Диаметр графа - это максимальное расстояние между парой вершин. Его также можно определить как максимальное расстояние между парой вершин. Чтобы решить эту проблему, нужно найти все пути, а затем найти их максимум.

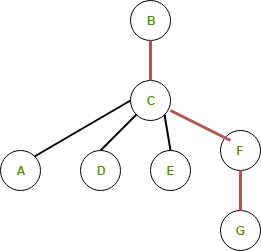
Диаметр: 3
BC → CF → FG

4. Радиус графа - Радиус графа существует, только если он имеет диаметр. Минимальное среди всех максимальных расстояний между вершиной и всеми остальными вершинами считается радиусом Графа G. Он обозначается как r (G).

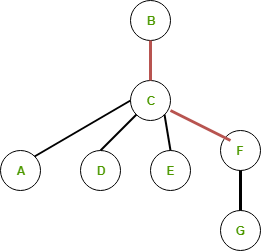
Радиус: 2
Все доступные минимальные радиусы: 
BC → CF,
BC → CE,
BC → CD,
BC → CA

5. Центр графика -
Он состоит из всех вершин, эксцентриситет которых минимален. Здесь эксцентриситет равен радиусу. Например, если школа находится в центре города, это сократит расстояние, которое придется преодолевать автобусам.

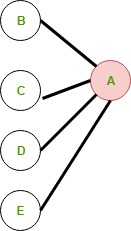
Центр: A

6. Эксцентриситет графика -
Он определяется как максимальное расстояние одной вершины от другой вершины. Максимальное расстояние между вершиной и всеми остальными вершинами считается эксцентриситетом вершины. Обозначается через e (V).

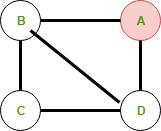
Эксцентриситет от:
(А, А) = 0
(А, В) = 1
(А, С) = 2
(A, D) = 1
Максимальное значение - 2, поэтому эксцентриситет - 2.