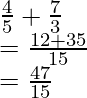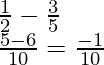Фракции

Фракция определяется как часть целого. Дробь часто используется не только в математике, но и в реальной жизни. Древние египтяне были первыми людьми, которые начали использовать дроби. Они использовали его в своих повседневных жизненных проблемах, таких как раздача еды и припасов. Слово «фракция» происходит от латинского слова «fractus», что в переводе с английского означает «сломанный», и соответствует значению дроби. Давайте узнаем подробно о дробях и их типах.

Что такое Фракция?

Фракции определяются как часть целого. Дроби — это числовое значение, которое может быть частью или частью любого количества, где количество может быть любым. Итак, дроби – это часть или часть величины. Ниже приведен пример дробей, пицца делится на 8 равных частей, и каждая часть является долей всей пиццы, поэтому части - это доли пиццы, то есть количество (целое). Если вынуть одну часть, она представляется как 1/8 в форме дроби. Дробь можно записать разными способами,

• Одна восьмая
• 1/8
• 1 на 8

Остальные части в совокупности будут составлять 7/8 пиццы на данный момент; осталось всего 7 шт. Точно так же, если вынуть 2 куска, они составят 2/8 всей пиццы. Его можно упростить и записать как 1/4.

Части дроби

Дробь состоит из двух частей, т. е. числителя и знаменателя. Число, указанное сверху, называется числителем, а число, расположенное внизу, называется знаменателем. Часть числителя определяет количество частей целого, тогда как знаменатель определяет общее количество равных частей в целом. Числитель и знаменатель разделены дробной чертой.

• Числитель : Числитель представляет часть дроби. Это верхняя часть дроби.
• Знаменатель : Знаменатель представляет собой целое, на которое делится дробь. Это нижняя часть дроби.

Операции над дробями

Операции с дробями — это простые арифметические операции, такие как сложение, умножение, деление и т. д. Давайте рассмотрим операции, которые мы можем выполнять с дробями:

Сокращение дробей

Сокращение дробей — это упрощение дробей путем деления числителя и знаменателя на одно и то же значение. Важно отметить, что деление их на 1 не изменит дробь.

Пример: уменьшить дробь ⇢ 88/42.

Решение:

88/42 is an improper fraction and both numerator and denominator are divisible by 2. Dividing them by 2:

88/42 = 44/21

Therefore, the reduced fraction becomes 44/21.

Умножение дробей

Умножение дробей не требует общего знаменателя. Здесь просто числитель умножается на числитель другой дроби, а знаменатель умножается на знаменатель. Его также можно упростить впоследствии, если дробь можно уменьшить. Дроби также могут быть упрощены при умножении друг на друга.

Пример: Как умножать дроби, дроби 21/5 и 35/12.

Решение:

Multiplying fractions:

Сложение дробей

Сложение дробей возможно только при одинаковом знаменателе, в случае, если знаменатели дробей не совпадают, важно привести их к общему знаменателю. Найдите НОК дробей, чтобы найти общий знаменатель.

Пример: Как сложить дроби 4/5 и 7/3.

Решение:

Here, the denominators of both fractions are not same, LCM of 3 and 5 is 15,

Разделение дробей

Для деления дробей не нужны общие знаменатели. Самый простой способ делить дроби — перевернуть дробь после знака деления, то есть сделать дробь обратным образом и изменить знак с деления на умножение. Теперь просто примените правила умножения дробей и решите.

Пример: Как разделить дроби 35/20 и 5/10.

Решение:

Dividing fractions: 35/20 ÷ 7/10

Flipping the fraction after division sign and changing the sign to multiplication sign:

35/20 × 10/7

Reducing the fractions:

7/4 × 10/7 = 70/28 = 10/4 = 5/2

Therefore, the answer is 5/2.

Вычитание дробей

Вычитание дробей возможно только при совпадении знаменателей. В случае, если знаменатели дробей не совпадают, важно привести их к общему знаменателю. Найдите НОК дробей, чтобы найти общий знаменатель.

Пример: Вычесть дроби 1/2 из 3/5.

Решение:

The least common denominator of 2 and 5 is 10. Solving:

Свойства дробей

У дробей есть некоторые важные свойства, подобные целым числам, натуральным числам и т. д. Давайте посмотрим на эти свойства:

• Для сложения дробей и умножения дробей верны коммутативные и ассоциативные свойства.
• Дробное умножение дает 1, а единичный элемент равен 0.
• Мультипликативное обратное свойство возвращает дробь. То есть a/b — это b/a, где a и b — ненулевые числа.
• Дистрибутивное свойство умножения над сложением верно для дробей.

Типы фракций

Есть в основном четыре типа фракций. Это единичные дроби, правильные дроби, неправильные дроби и смешанные дроби. Они классифицируются на основе их числителя и знаменателя. Давайте узнаем обо всех четырех типах подробно:

Доля единицы

Единичная дробь определяется как дробь с 1 в качестве числителя и известна как единичная дробь, например — 1/8, 1/10, 1/4, 1/6, 1/11 и т. д. Можно сказать что все единичные дроби являются правильными дробями, поскольку все единичные дроби имеют 1 в числителе, что меньше знаменателя. Приведенный ниже пример очень хорошо объясняет дробь единицы. Здесь торт делится на 4 равные части. Если весь торт равен 1, то каждая четверть торта — это дробь 1/4.

Правильная дробь

Правильная дробь определяется как дробь, в которой значение числителя меньше значения знаменателя. Она известна как правильная дробь, например, 4/9, 1/10, 2/5, 3/7, 5/9 и т. д.

Неделимая дробь

Неправильная дробь определяется как дробь, в которой значение числителя больше значения знаменателя, тогда она известна как неправильная дробь, например, 6/5, 11/10, 11/5, 5/3, 2/ 1 и т.д.

Смешанная фракция

Смешанная дробь состоит из целого числа с правильной дробью, тогда она известна как смешанная дробь. Например, если 2 — целое число, а 1/4 — дробь, то 2¼ — смешанная дробь.

Другие типы фракций

Другие виды фракций строятся на основе групп. Они включают в себя подобные и неодинаковые дроби и эквивалентные дроби. Ниже подробно описаны все три типа дробей.

Как дроби

Две или более двух дробей с одинаковыми знаменателями называются как дроби. Примеры подобных дробей:

1. 2/9, 3/9, 5/9, 9/9, 4/9 (Здесь знаменатели у всех дробей одинаковые, то есть 9).
2. 3/10, 7/10, 1/10, 9/10, 6/10 (Здесь знаменатели у всех дробей одинаковые, то есть 10).
3. 1/7, 2/7, 4/7, 5/7, 7/7, 8/7.
4. 1/2, 7/2, 6/2, 5/2, 9/2.
5. 7/5, 1/5, 4/5, 3/5.

В отличие от дробей

Дроби с разными знаменателями называются неодинаковыми. Пример, в отличие от дробей,

1. 9/2, 1/6, 5/4, 7/3 (Здесь знаменатель у всех дробей разный).
2. 1/2, 1/4, 2/3, 5/6, 8/9 (Здесь знаменатель у всех дробей разный).
3. 3/8, 2/3, 3/5, 2/7.
4. 1/9, 2/7, 3/4, 2/5, 3/2.
5. 4/2, 1/6, 2/3, 7/5.

Эквивалентные дроби

Равнозначные дроби определяются как те дроби, которые дают одно и то же значение после упрощения, и тогда они эквивалентны друг другу. Решение равнозначных дробей может быть выполнено либо путем умножения числителя и знаменателя на одно и то же число, либо путем деления числителя и знаменателя на одно и то же число. Ниже приведены некоторые примеры эквивалентных дробей:

Пример: Найдите две равные дроби числа 4/12.

Решение:

Equivalent fraction by multiplying with the same number, lets multiply by 2:

(4 × 2)/(12 × 2)

= 8/24

Equivalent fraction by division with the same number, here, both numerator and denominator are divisible by 4, dividing by 4:

(4 ÷ 4)/(12 ÷ 4)

= 1/3

Дробь на числовой прямой

Дроби на числовой прямой изображаются между интервалом двух целых чисел. Дробь – это часть целого. Следовательно, целое делится на равные части, количество частей между целыми числами определяется значением знаменателя, а значением числителя является точка, в которой лежит дробь. Например, если нам требуется представить 1/8 на числовой прямой, деление будет между 0 и 1, а так как 8 в знаменателе, то целое делится на 8 равных частей, где первая представляет 1/8 . Точно так же вторая часть представляет 2/8 и так далее.

Как преобразовать дроби в десятичные?

Десятичные числа — это числа, представляющие дроби, но в десятичной форме. Например, 1/4 дроби можно записать как 0,25 в десятичной форме. Десятичные числа в основном предпочтительнее, так как их можно использовать для множества математических операций, где решение дробей кажется сложным, например, сложение, вычитание и т. д. Например: чтобы сложить 1/2 и 1/4, проще решать десятичные дроби. . Преобразование дробей в десятичные ⇢ 0,5 + 0,25 = 0,75.

Как преобразовать десятичную дробь в дробь?

Десятичные числа преобразуются в десятичные, поскольку иногда математические операции легко решаются в форме дробей. Математические операции, такие как умножение и деление, иногда проще выполнять с дробями. Ниже приведены шаги, которые можно выполнить, чтобы преобразовать десятичную дробь в дробь:

• Преобразуйте десятичную дробь в форму p/q, где q = 1.
• Теперь умножьте числитель и знаменатель на 10, пока числитель не станет целым числом из десятичных знаков. Например, если после запятой два числа, умножьте 100/100.
• Теперь упростим полученную дробь.

Значение числа Пи в дробях

Пи (π) — математическая константа, определяемая как отношение длины окружности к ее диаметру. Значение числа пи в десятичном виде примерно равно 3,14. Значение числа пи (π) в дробях равно 22/7. Значение числа пи используется как в десятичной, так и в дробной форме в зависимости от типа заданного вопроса.

Например: Преобразуйте 0,8 в дробь.

• Convert into p/q form ⇢ 0.8/1
• Multiply 10/10 ⇢ 0.8/1 × 10/10
• Simplifying fraction ⇢ 8/10 = 4/5.

Решенные примеры на дроби

Вопрос 1: Напишите две равные дроби 3/39.

Решение:

Equivalent fraction by multiplying with the same number, lets multiply by 2:

(3 × 2)/(39 × 2)

= 6/78

Equivalent fraction by division with the same number, here, both numerator and denominator are divisible by 3, dividing by 3:

(3 ÷ 3)/(39 ÷ 3)

= 1/13

Вопрос 2: В классе из 90 учеников 1/3 учеников не любит крикет. Сколько студентов любят крикет?

Решение:

Fraction of students that do not like cricket = 1/3

Fraction of student that like cricket = 1 – 1/3

= (3 – 1)/3

= 2/3rd students like cricket.

Number of students that like cricket = 2/3 × 90

= (2 × 30)

= 60 

Therefore, 60 students like cricket.

Вопрос 3: Что это за дробь – 1/2, 1/5, 1/7, 1/10, 1/3?

Отвечать:

This is a Unit fraction because all the fractions have 1 as a numerator. 

Вопрос 4: Определите вид дроби 7¼.

Отвечать:

Mixed fraction because it is a combination of both whole number and a proper fraction in which 7 is the whole number and 1/4 is the proper fraction.

Вопрос 5: Чему равна дробь 7/5?

Отвечать:

To find the equivalent fraction of 7/5, we need to multiply both numerator and denominator by the same number.

Hence, (7/5) × (2/2) = 14/10

Therefore equivalent fraction of 7/5 is 14/10.

Часто задаваемые вопросы о дробях

Вопрос 1: Что такое сравнение дробей?

Отвечать:

Comparing fractions is done to understand which fraction is larger or which fraction is smaller among the given fractions. If the denominator of the fractions given are same, only the numerators are compared, if the fractions have different denominators, first the LCM of fractions are taken, and then the numerators are compared. For example, 3/19 and 7/19 when compared, it can be observed that the denominator are same, therefore, numerators are compared, 3 > 7, therefore, 7/19 > 3/19.

Вопрос 2: Как умножать дроби?

Ответы:

Multiplication of fraction do not require any common denominator. Here, simply the numerator is multiplied by numerator of the other fraction and denominator is multiplied by the denominator. It can also be simplified afterwards if the fraction can be reduced. Fractions can also be simplified while multiplying with each other. For example: 3/7 × 1/2 = 3/14.

Вопрос 3: Как делить дроби?

Отвечать:

Division of fractions do not require any common denominators, the simplest way to divide fractions is to flip the fraction after division sign, that is, reciprocate the fraction, and change the sign from division to multiplication. Now, simply apply the multiplication of fractions rules and solve. For example: 4/9 ÷ 2/3 = 4/9 × 3/2 = 2/3.

Вопрос 4: Как складывать дроби?

Отвечать:

Adding fractions is possible only when the denominator are same, incase the denominators of the fractions are not same, it is important to bring them to a common denominator. Find the LCM of fractions in order to find the common denominator. For example: 3/4 + 1/2 = 3/4 + 2/4 = 5/4.

Вопрос 5: Что такое неправильная дробь?

Отвечать:

An Improper fraction is defined as a fraction in which the numerator value is greater than the denominator value, then it is known as an improper fraction, for example, 7/5, 13/10, 9/5, 17/3, 5/1, etc.

Вопрос 6: Какую часть суток составляют 8 часов?

Отвечать:

We know that 1 day has 24 hours.

1 hour = 1/24 days

8 hours = 1/24 × 8 days

8 hours = 8/24 = 1/3 days

Therefore, 8 hours has 1/3 days.

Статьи по Теме

• Whole Numbers
• Natural Numbers
• Real Numbers