Формулы четырехугольника

Четырехугольник — это замкнутая фигура и тип многоугольника, который имеет четыре стороны или ребра, четыре угла и четыре угла или вершины. Слово «четырехугольник» происходит от латинских слов «quad», варианта «четыре», и «latus», что означает сторона. Его также называют тетрагоном , происходящим от греческого слова «тетра», означающего четыре, и «гон», означающего угол или угол.

Четырехугольник образован соединением четырех не лежащих на одной прямой точек. Сумма внутренних углов четырехугольника всегда равна 360 градусам.

Не обязательно, чтобы все четыре стороны четырехугольника были равны по длине. Таким образом, у нас могут быть разные типы четырехугольников в зависимости от их сторон и углов.

Здесь ABCD - четырехугольник с четырьмя сторонами, а именно AB, BC, CD, DA, четырьмя углами ∠A, ∠B, ∠C, ∠D, а линии, соединяющие A с C и B с D, являются двумя диагоналями четырехугольника .

Виды четырехугольника

1. Параллелограмм
2. Прямоугольник
3. Площадь
4. Ромб
5. Трапеция
6. Летающий змей

Параллелограмм

Параллелограмм – это четырехугольник с двумя парами параллельных сторон. Противоположные стороны параллелограмма имеют одинаковую длину, и противоположные углы параллелограмма также равны.

Прямоугольник

Прямоугольник — это тип четырехугольника, у которого параллельные стороны равны друг другу, а все четыре угла равны 90°. Поэтому его еще называют равноугольным четырехугольником.

Площадь

Четырехугольник с четырьмя равными сторонами и четырьмя равными углами называется квадратом .

Ромб

Ромб — это тип параллелограмма с четырьмя равными сторонами и равными противоположными углами.

Трапеция

Трапеция — это разновидность четырехугольника, у которого только одна пара сторон параллельна друг другу.

Видеть

Четырехугольник, у которого две смежные стороны равны, известен как воздушный змей .

Формулы четырехугольника

Есть две основные формулы для четырехугольников

1. Область
2. Периметр

Площадь четырехугольников

В геометрии площадь может быть определена как пространство, занимаемое плоской формой или поверхностью объекта. Площадь фигуры — это количество единичных квадратов, покрывающих поверхность замкнутой фигуры. Площадь измеряется в квадратных единицах, таких как квадратные сантиметры, квадратные футы, квадратные дюймы и т. д.

Area of Parallelogram = Base × Height

Area of Rectangle = Length × Width

Area of Square = Side × Side

Area of Rhombus = 1/2 × diagonal1 × diagonal2 

Area of Trapezium = 1/2 × Height × (Length1 + Length2)

Area of Kite = 1/2 ×diagonal1 × diagonal2

Периметр четырехугольников

В геометрии периметр можно определить как путь или границу, окружающую фигуру. Его также можно определить как длину контура фигуры.

Поскольку мы знаем, что у четырехугольника четыре стороны, периметр любого четырехугольника, скажем, ABCD, равен

Perimeter = AB + BC + CD + DA (sum of all the sides)

Perimeter of Parallelogram = 2×(Base + Side)

Perimeter of Rectangle = 2×(Length + Width)

Perimeter of Square = 4 × Side

Perimeter of rhombus = 4 × Side

Perimeter of Trapezium = Sum of all the sides

Perimeter of Kite = 2×(a + b), where a, and b are adjacent pairs

Примеры проблем

Задача 1: Если 20см и 10см - длины диагоналей воздушного змея, то найдите площадь воздушного змея.

Решение:

Given : 

Length of diagonal1 = 20cm

Length of diagonal2 = 10cm

Area of Kite =1/2 × diagonal1 × diagonal2

Area =1/2 ×20 ×10 = 100cm²

Задача 2: Как найти периметр неправильного четырехугольника?

Решение:

To determine the perimeter of an irregular quadrilateral we can simply add the length of the outer sides of the quadrilateral. Because perimeter is nothing but the total length of the periphery of any shape.

Задача 3: Найдите площадь трапеции, длина параллельных сторон которой равна 7 см и 18 см соответственно, а высота трапеции равна 10 см.

Решение:

Given,

Length of parallel sides of Trapezium,

Length 1 = 7cm

Length 2 = 18cm

Height of Trapezium = 10cm

we know that, Area of Trapezium = 1/2 × Height × (Length1 + Length2)

Therefore,

Area = 1/2 × 10 ×(7 +18)

          =125cm²

Hence, Area of the given trapezium is 125cm²

Задача 4: периметр четырехугольника равен 90 см, а длины трех сторон равны AD = 23 см, AB = 28 см и BC = 18 см. Найдите длину четвертой стороны, т.е. CD.

Решение:

Given,

Length of side AB = 28cm

Length of side BC = 18cm

Length of side AD = 23cm

Let the length of side CD = x cm

we know that,

Perimeter = AB + BC + CD + AD

This implies,

90 = 28 + 18 + x +23

90 = 69 + x

x = 21

Hence, the length of side AD = 21cm 

Задача 5: Если площадь ромба 70 см ² , а основание 15 см, то найдите высоту данного ромба.

Решение:

Area = 70cm²

Base = 15cm

Since Area of Rhombus = Height × Base

This implies, 

70 = Height × 15

Height = 70/15

Height = 4.67cm

Задача 6: Запишите формулу для вычисления длины диагонали прямоугольника.

Решение:

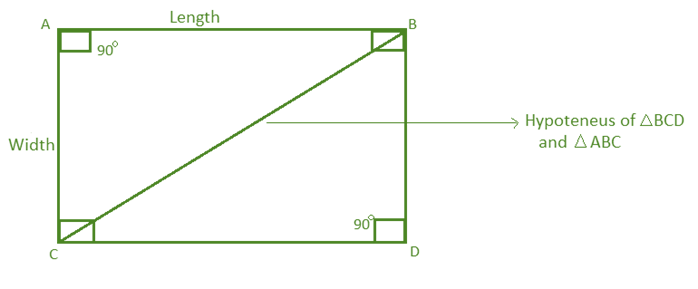
The diagonal of a rectangle is a line segment drawn to connect any two non-adjacent vertices of a rectangle. A rectangle can have a maximum of two diagonals of equal length.

A diagonal rectangle divides the rectangle into two right-angle triangles. Therefore we can easily calculate the length of diagonals using the Pythagoras Theorem, where the diagonals are considered as the hypotenuse of the right triangle.

 

Consider triangle BCD,

Since the triangle BCD is a right angle triangle,

Therefore, (BC)² = (BD)² + (CD)²

                 (BC)² = (width)² + (length)² 

                  BC = √(width)² + (length)²

Задача 7: Найдите периметр параллелограмма, основание которого равно 12 см, а высота 23 см.

Решение:

Base length of given parallelogram = 12cm

Height of given parallelogram = 23cm

Perimeter of a parallelogram = 2×(a + b)

where a = 12cm and b = 23cm

Perimeter of parallelogram = 2×(12 + 23)

                                            = 70cm

Hence, the perimeter of the given parallelogram is 70cm