Формула теоремы Пифагора

Теорема Пифагора, также известная как теорема Пифагора, может быть определена как отношение между тремя сторонами (гипотенуза, основание, перпендикуляр) прямоугольного треугольника. Он гласит, что сумма квадратов двух меньших сторон (основания и перпендикуляра) равна квадрату наибольшей стороны (гипотенузы).

Эта теорема названа в честь греческого философа Пифагора, родившегося около 570 г. до н.э.

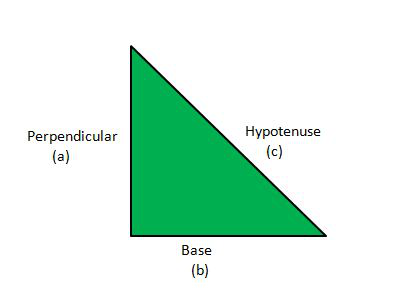
Формула теоремы Пифагора

a² + b²  = c²

Here c is denoting the length of the hypotenuse and a and b are denoting the lengths of the perpendicular and the base.

Therefore,

Hypotenuse² = Perpendicular² + Base²

Пример: Возьмем прямоугольный треугольник со сторонами 3, 4, 5, теперь докажем теорему Пифагора.

Решение:

Sum of squares of two small sides = 3² + 4² = 25

Square of the longest side = 5² = 25

Hence we can see that

sum of squares of two small sides = square of the longest side        

                                                25 = 25

Теорема Пифагора показывает отношение сторон прямоугольного треугольника, поэтому, если длина какой-либо стороны отсутствует, ее можно вычислить с помощью теоремы Пифагора.

Если даны длины как a (перпендикуляра), так и b (основания), то длину c можно рассчитать по формуле:

c = √(a² + b²)

Similarly a and b can also be calculated if those are missing.

Примеры вопросов

Вопрос 1: Найдите гипотенузу прямоугольного треугольника, основание которого равно 6 см, а высота 8 см?

Отвечать:

Using Pythagorean theorem, a² + b² = c²

So 6² + 8² = c² 

hence c = √(36 + 64)

          c = √100

          c = 10 cm

Вопрос 2: Определите, является ли данный треугольник прямоугольным или нет, стороны равны 6, 8, 12?

Отвечать:

A right-angled triangle follows the Pythagorean theorem so let’s check it.

Sum of squares of two small sides should be equal to the square of the longest side

So 6² + 8² must be equal to 12²

but 36 + 64 =100 while 12² = 144

Hence it is not a right angled triangle as it is not satisfying the Pythagorean theorem.

Вопрос 3: Найдите основание прямоугольного треугольника, гипотенуза которого равна 13 см, а высота 12 см?

Отвечать:

Using Pythagorean theorem, a² + b² = c²

a(perpendicular)= 12, c(hypotenuse) = 13, find b(base)

So b = √(c² – a²)

hence b = √(169 – 144)

           b = √25

           b = 5 cm

Вопрос 4: Найдите перпендикуляр к прямоугольному треугольнику, гипотенуза которого равна 25 см, а основание равно 7 см?

Отвечать:

Using Pythagorean theorem, a² + b² = c²

b(base)= 7, c(hypotenuse) = 25, find a(perpendicular)

so a = √(c² – b²)

hence a = √(625 – 49)

          a = √576

          a = 24 cm

Вопрос 5: Определите, является ли данный треугольник прямоугольным или нет, стороны равны 10, 24, 26?

Отвечать:

A right-angled triangle follows the Pythagorean theorem so let’s check it.

Sum of squares of two small sides should be equal to the square of the longest side

so 10² + 24² must be equal to 26²

100 + 576 = 676 which is equal to 26² = 676

Hence the given triangle is a right-angled triangle because it is satisfying the Pythagorean theorem.