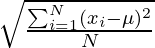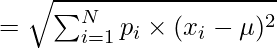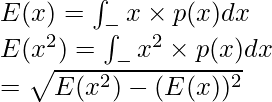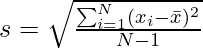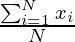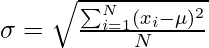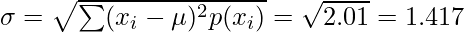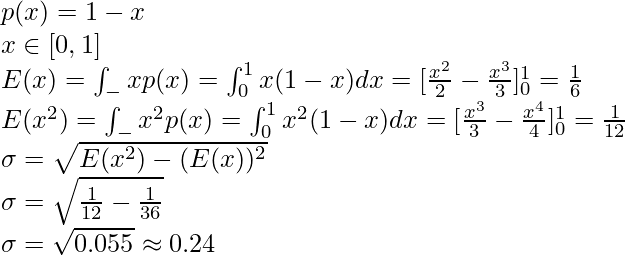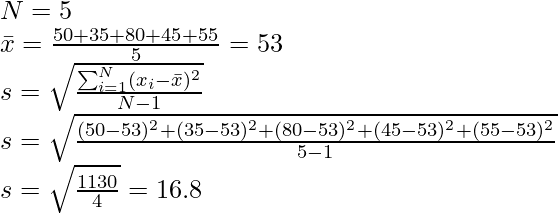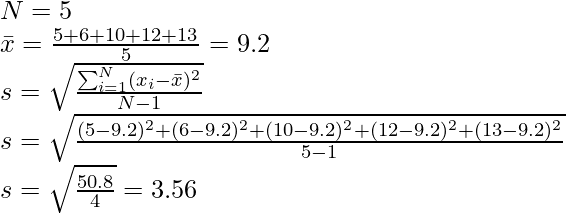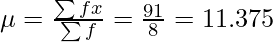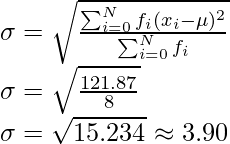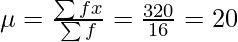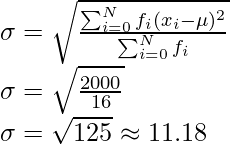Формула стандартного отклонения
В статистике мера вариации значений известна как стандартное отклонение (SD). Низкое значение SD означает, что данный набор значений разбросан по небольшому диапазону, тогда как большое значение SD означает, что набор значений разбросан по большому диапазону. SD часто обозначается греческим алфавитом sigma σ для стандартного отклонения совокупности или буквой s для стандартного отклонения выборки. Теперь мы увидим, в чем разница между популяцией и выборкой и в чем разница между их стандартными отклонениями. Население определяется как вся группа, которую вы хотите изучить. Например, все футболисты футбольного клуба «Ливерпуль», все страны мира и все смартфоны мира. Выборка определяется как подгруппа совокупности при определенных условиях. Например, все нападающие футбольного клуба «Ливерпуль», все страны с существующей монархией, все смартфоны производства Apple.
Население против выборки
Примечание. Размер выборки обычно меньше размера генеральной совокупности, но в некоторых редких случаях он может быть таким же. Теперь, когда мы знаем разницу между популяцией и выборкой, давайте посмотрим на их стандартные отклонения.
Формула стандартного отклонения населения
σ =
Here σ = Population Standard Deviation
xi = ith observation
μ = mean of N observation
N = number of observations.
Если x i имеет разные вероятности, мы используем формулу
Where pi = probability of xi
Приведенные выше формулы используются, когда значение x конечно. Если нам дан непрерывный диапазон x , мы используем следующее:
Here p(x) = Probability density function
E(x) = mean or expected value
Стандартное отклонение выборки
Формула SD выборки очень похожа на SD популяции с небольшими изменениями.
Here
= mean of the sample
N = number of sample
Откуда берется Н-1?
Значения в выборке, естественно, будут ближе к среднему значению выборки. 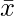 чем к среднему населению μ. Таким образом, чтобы компенсировать это, чтобы стандартное отклонение не было занижено, мы используем N – 1 вместо N в знаменателе. Если кто-то хочет прочитать об этом дальше, не стесняйтесь гуглить Непредвзятая оценка стандартного отклонения. Это даст вам причину, по которой мы используем N – 1, а не N – 2 и т. д.
чем к среднему населению μ. Таким образом, чтобы компенсировать это, чтобы стандартное отклонение не было занижено, мы используем N – 1 вместо N в знаменателе. Если кто-то хочет прочитать об этом дальше, не стесняйтесь гуглить Непредвзятая оценка стандартного отклонения. Это даст вам причину, по которой мы используем N – 1, а не N – 2 и т. д.
Стандартное отклонение сгруппированных данных
Теперь посмотрим, что делать, если вам дали сгруппированные данные вместе с их частотой появления. В дискретном частотном распределении одно значение X соответствует одной частоте. Из приведенных ниже примеров задач станет ясно,
Примеры проблем
Задача 1: найти стандартное отклонение X = {2, 2, 3, 4, 6, 7}.
Решение:
N = 6
x = {2, 2, 3, 4, 6, 7}
μ =
= (2 + 2 + 3 + 4 + 6 + 7)/ 6
= 4
= (2 – 4)2 + (2 – 4)2 + (3 – 4)2 + (4 – 4)2 + (6 – 4)2 + (7 – 4)2
= 22
σ = √(22/6)
= 1.914
Задача 2: найти стандартное отклонение X = {0, 1, 2, 3, 4}, где вероятность каждого значения определяется выражением p(x) = {0,1, 0,3, 0,1, 0,2, 0,3}.
Решение:
X
p(X)
(A)
X × p(X)
(Xi – μ)2
(B)
A×B
0
0.1
0
5.29
0.529
1
0.3
0.3
1.69
0.507
2
0.1
0.2
0.09
0.009
3
0.2
0.6
0.49
0.098
4
0.3
1.2
2.89
0.867
Total
2.3
2.01
μ = ∑ p(x) × x
= 2.3
Задача 3: найти стандартное отклонение X, если PDF X задается функцией p(x) = (1 – x) для x ∈ [0, 1].
Решение:
Задача 4: В классе было 30 учеников. Вес 5 указан следующим образом: 50 кг, 35 кг, 80 кг, 45 кг и 55 кг. Найдите стандартное отклонение выборки.
Решение:
Задача 5: Найдите образец SD следующих данных — {5, 6, 10, 12, 13}
Решение:
Задача 6. Найдите стандартное отклонение следующих данных:
Х я | я |
5 | 2 |
12 | 4 |
15 | 3 |
Решение:
Xi fi Xi×fi Xi-μ (Xi-μ)2 f×(Xi-μ)2 5 2 10 -6.375 40.64 81.28 12 3 36 0.625 0.39 1.17 15 3 45 3.625 13.14 39.42 Total 8 91 121.87
Задача 7. Найдите стандартное отклонение следующей таблицы данных.
| Учебный класс | ф |
| 0-10 | 3 |
| 10-20 | 6 |
| 20-30 | 4 |
| 30-40 | 2 |
| 40-50 | 1 |
Решение:
Class
Mid point
Xi
f
f×Xi
Xi – μ
(Xi – μ)2
f×(Xi – μ)2
0-10
5
3
15
-15
225
675
10-20
15
6
90
-5
25
150
20-30
25
4
100
5
25
100
30-40
35
2
70
15
225
450
40-50
45
1
45
25
625
625
Total
16
320
2000