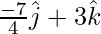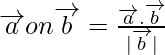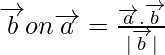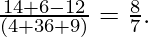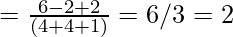Формула скалярной и векторной проекции

Перед векторной проекцией мы должны взглянуть на скалярную проекцию или, как правило, мы говорим о проекции 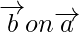, означает вектор 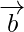производит проекцию на вектор 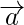. Проекции в основном бывают двух типов: скалярные проекции и векторные проекции. Скалярная проекция говорит нам о величине проекции, а векторная проекция говорит нам о себе и об единичном векторе проекции.

Проекция

Рассмотрим два вектора 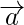и эти два вектора близки друг к другу с одной стороны и образуют угол θ между ними. Вектор 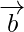делает проекцию на вектор 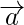. Для лучшего понимания вы можете предположить, что есть две палочки, как положение вектора. мы ставим факел на условие над вектором 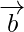. Затем вы видите тень на первом векторе палочки. 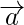эта тень является проекцией второй палки (вектор 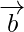) на первой палке ( ).

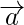Скалярная проекция

Projection of

Сходным образом,

Projection of

Векторная проекция

Векторная проекция определяется как произведение скалярной проекции 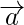на 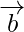и единичный вектор вдоль 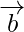. Векторная проекция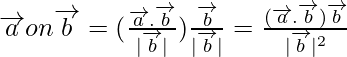

Сходным образом,

Векторная проекция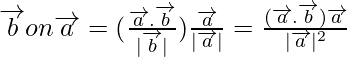

Примеры проблем

Проблема 1: Если 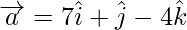[Текс] [/Текс] и 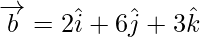[Текс] [/Текс] . затем найдите проекцию вектора a на b.

Решение :

Here,   and              Projection of  =              

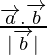
Projection of  =             

= 

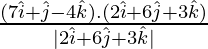
Задача 2: найти проекцию вектора a + b на вектор c, здесь 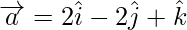, 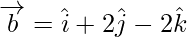а также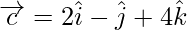

Решение:

Here,   , and          

            

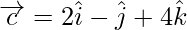
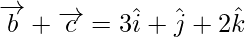
Projection of vector  on         

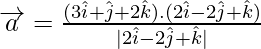
Задача 3: найти проекцию вектора a на b, здесь 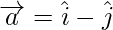а также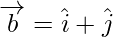

Решение:

Let  and             

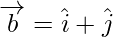
Projection of   =             

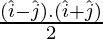
=  =  0

Задача 4: Найдите скалярную проекцию a на b, здесь overrightarrow{a} = 2hat{i} – hat{j} + hat{k}, overrightarrow{b} = hat{i} -2шляпа{j} +шляпа{к}

Решение:

Let  and            

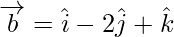
Projection of   =             

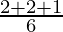
= 5/6

Задача 5. Найдите значение λ, когда скалярная проекция a на b равна 4, здесь ,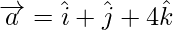

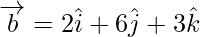
Решение :

Here,  Projection of          

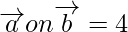
 and              

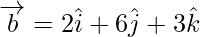
Projection of  on  =            

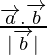
4  =            

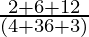
4 =            

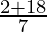
28 = 2λ + 18           

λ = 5

Задача 6: Проекция вектора a на b, здесь 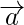знак равно 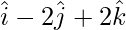а также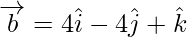

Решение:

=  and                 

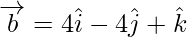
Projection of the vector                

= 

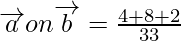
Задача 7: найти векторную проекцию m на вектор n, здесь 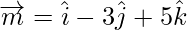а также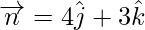

Решение:

Here,  and             

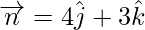
Vector projection=             

=
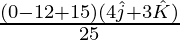