Длина самого длинного подотрезка, который становится UpDown после вставки не более одного целого числа

Опубликовано: 5 Января, 2022

Последовательность целых чисел 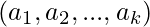называется UpDown, если выполняется неравенство 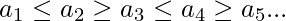Справедливо.
Вам дана последовательность . В последовательность можно вставить не более одного целого числа. Это может быть любое целое число. Найдите длину самого длинного подотрезка новой последовательности после добавления целого числа (или отказа от него), равного UpDown.
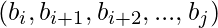Подотрезок - это последовательная часть последовательности. То есть подотрезок будет иметь форму для некоторых 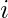а также .
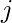Эту проблему задавали на олимпиаде по зональным вычислениям 2019.
Примеры:

Input: arr[] = {1, 10, 3, 20, 25, 24}
Output: 7
Suppose we insert 5 between 20 and 25, the whole sequence (1, 10, 3, 20, 5, 25, 24)
becomes an UpDown Sequence and hence the answer is 7.
Input: arr[] = {100, 1, 10, 3, 4, 6, 11}
Output: 6
Suppose we insert 4 between 4 and 6, the sequence (1, 10, 3, 4, 4, 6) becomes an UpDown
Sequence and hence the answer is 6. We can verify that this is the best possible
solution.

Рекомендуется: сначала попробуйте свой подход в {IDE}, прежде чем переходить к решению.

Подход: давайте начнем с определения двух типов последовательности:

UpDown Sequence (UD): последовательность формы То есть последовательность начинается с увеличения.
DownUp Sequence (DU): последовательность в форме 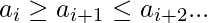То есть последовательность начинается с убывания.

Давайте сначала выясним длину последовательностей UD и DU, не задумываясь о других частях проблемы. Для этого определим быть самой длинной последовательностью UpDown, начинающейся в 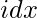а также 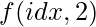быть самой длинной последовательностью DownUp, начиная с .
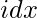Отношение рекуррентности для 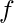является :-

(1)

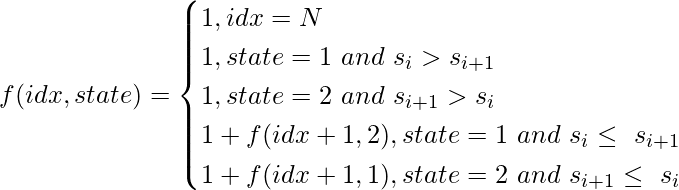
Здесь N - длина последовательности, а состояние равно 1 или 2 и означает последовательность UD и DU соответственно. При формировании рекуррентного соотношения мы использовали тот факт, что в UD-последовательности 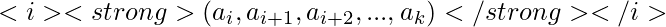, часть является последовательностью DU и наоборот . Мы можем использовать динамическое программирование для вычисления значения 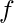а затем сохраните наш результат в массиве dp [N] [2] .
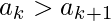Теперь обратите внимание, что всегда можно вставить целое число в конце последовательности UpDown, чтобы увеличить длину последовательности на 1 и при этом сохранить неравенство UpDown. Почему ? Предположим, что последовательность UD прерывается в потому что когда мы ожидали, что это будет 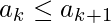. Мы можем вставить целое число между а также 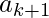. Теперь, 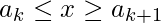доволен.
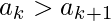Мы можем привести аналогичные аргументы для случая, когда последовательность UD прерывается при потому что когда мы ожидали, что это будет 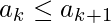. Но на самом деле нам не нужно ничего вставлять. Нам нужно просто найти длину самой длинной возможной последовательности UD.
Обратите внимание, что последовательность UD представляет собой комбинацию:

UD-последовательность I + x + UD-последовательность II, если длина UD-последовательности I нечетная
Последовательность UD I + x + последовательность DU I, если длина последовательности UD I четная

где x - вставленный элемент.
Итак, для каждого i мы вычисляем длину самой длинной последовательности UD, начиная с i. Пусть эта длина равна y.
Если y нечетное, мы вставляем туда элемент (теоретически) и вычисляем длину самой длинной последовательности UD, начиная с i + y. Самая длинная последовательность UD, начинающаяся с i после вставки элемента, поэтому dp [i] [1] + 1 + dp [i + y] [1] .
Если y четно, мы вставляем туда элемент (теоретически) и вычисляем длину самой длинной последовательности DU, начиная с i + y. Самая длинная последовательность UD, начинающаяся с i после вставки элемента, поэтому dp [i] [1] + 1 + dp [i + y] [2] .
Окончательный ответ - максимальное такое значение среди всех i.

C ++

 // C++ implementation of the approach
 #include <bits/stdc++.h>
 using namespace std;
 // Function to recursively fill the dp array
 int f( int i, int state, int A[], int dp[][3], int N)
 {
    if (i >= N)
        return 0; 
    // If f(i, state) is already calculated
    // then return the value
    else if (dp[i][state] != -1) {
        return dp[i][state];
    }
    // Calculate f(i, state) according to the
    // recurrence relation and store in dp[][]
    else {
        if (i == N - 1)
            dp[i][state] = 1;
        else if (state == 1 && A[i] > A[i + 1])
            dp[i][state] = 1;
        else if (state == 2 && A[i] < A[i + 1])
            dp[i][state] = 1;
        else if (state == 1 && A[i] <= A[i + 1])
            dp[i][state] = 1 + f(i + 1, 2, A, dp, N);
        else if (state == 2 && A[i] >= A[i + 1])
            dp[i][state] = 1 + f(i + 1, 1, A, dp, N);
        return dp[i][state];
    }
 }
 // Function that calls the resucrsive function to
 // fill the dp array and then returns the result
 int maxLenSeq( int A[], int N)
 {
    int i, tmp, y, ans; 
    // dp[][] array for storing result
    // of f(i, 1) and f(1, 2)
    int dp[1000][3]; 
    // Populating the array dp[] with -1
    memset (dp, -1, sizeof dp); 
    // Make sure that longest UD and DU
    // sequence starting at each
    // index is calculated
    for (i = 0; i < N; i++) {
        tmp = f(i, 1, A, dp, N);
        tmp = f(i, 2, A, dp, N);
    }
    // Assume the answer to be -1
    // This value will only increase
    ans = -1;
    for (i = 0; i < N; i++) { 
        // y is the length of the longest
        // UD sequence starting at i
        y = dp[i][1];
        if (i + y >= N)
            ans = max(ans, dp[i][1] + 1);
        // If length is even then add an integer
        // and then a DU sequence starting at i + y
        else if (y % 2 == 0) {
            ans = max(ans, dp[i][1] + 1 + dp[i + y][2]);
        }
        // If length is odd then add an integer
        // and then a UD sequence starting at i + y
        else if (y % 2 == 1) {
            ans = max(ans, dp[i][1] + 1 + dp[i + y][1]);
        }
    }
    return ans;
 }
 // Driver code
 int main()
 {
    int A[] = { 1, 10, 3, 20, 25, 24 };
    int n = sizeof (A) / sizeof ( int ); 
    cout << maxLenSeq(A, n);
    return 0;
 }

Джава

 // Java implementation of the approach
 class GFG
 {
    
    // Function to recursively fill the dp array
    static int f( int i, int state, int A[],
                 int dp[][], int N)
    {
        if (i >= N)
            return 0 ;
    
        // If f(i, state) is already calculated
        // then return the value
        else if (dp[i][state] != - 1 )
        {
            return dp[i][state];
        }
    
        // Calculate f(i, state) according to the
        // recurrence relation and store in dp[][]
        else
        {
            if (i == N - 1 )
                dp[i][state] = 1 ;
            else if (state == 1 && A[i] > A[i + 1 ])
                dp[i][state] = 1 ;
            else if (state == 2 && A[i] < A[i + 1 ])
                dp[i][state] = 1 ;
            else if (state == 1 && A[i] <= A[i + 1 ])
                dp[i][state] = 1 + f(i + 1 , 2 , A, dp, N);
            else if (state == 2 && A[i] >= A[i + 1 ])
                dp[i][state] = 1 + f(i + 1 , 1 , A, dp, N);
            return dp[i][state];
        }
    }
    
    // Function that calls the resucrsive function to
    // fill the dp array and then returns the result
    static int maxLenSeq( int A[], int N)
    {
        int i,j, tmp, y, ans;
    
        // dp[][] array for storing result
        // of f(i, 1) and f(1, 2)
        int dp[][] = new int [ 1000 ][ 3 ];
        
        // Populating the array dp[] with -1
        for (i= 0 ; i < 1000 ; i++)
            for (j = 0 ; j < 3 ; j++)
                dp[i][j] = - 1 ; 
        // Make sure that longest UD and DU
        // sequence starting at each
        // index is calculated
        for (i = 0 ; i < N; i++)
        {
            tmp = f(i, 1 , A, dp, N);
            tmp = f(i, 2 , A, dp, N);
        }
    
        // Assume the answer to be -1
        // This value will only increase
        ans = - 1 ;
        for (i = 0 ; i < N; i++)
        {
    
            // y is the length of the longest
            // UD sequence starting at i
            y = dp[i][ 1 ];
    
            if (i + y >= N)
                ans = Math.max(ans, dp[i][ 1 ] + 1 );
    
            // If length is even then add an integer
            // and then a DU sequence starting at i + y
            else if (y % 2 == 0 )
            {
                ans = Math.max(ans, dp[i][ 1 ] + 1 + dp[i + y][ 2 ]);
            }
    
            // If length is odd then add an integer
            // and then a UD sequence starting at i + y
            else if (y % 2 == 1 )
            {
                ans = Math.max(ans, dp[i][ 1 ] + 1 + dp[i + y][ 1 ]);
            }
        }
        return ans;
    }
    
    // Driver code
    public static void main (String[] args)
    {
        int A[] = { 1 , 10 , 3 , 20 , 25 , 24 };
        int n = A.length;
    
        System.out.println(maxLenSeq(A, n));
    }
 }
 // This code is contributed by AnkitRai01

Python3

 # Python3 implementation of the approach
 # Function to recursively fill the dp array
 def f(i, state, A, dp, N):
    if i > = N:
        return 0 
    # If f(i, state) is already calculated
    # then return the value
    elif dp[i][state] ! = - 1 :
        return dp[i][state] 
    # Calculate f(i, state) according to the
    # recurrence relation and store in dp[][]
    else :
        if i = = N - 1 :
            dp[i][state] = 1
        elif state = = 1 and A[i] > A[i + 1 ]:
            dp[i][state] = 1
        elif state = = 2 and A[i] < A[i + 1 ]:
            dp[i][state] = 1
        elif state = = 1 and A[i] < = A[i + 1 ]:
            dp[i][state] = 1 + f(i + 1 , 2 , A, dp, N)
        elif state = = 2 and A[i] > = A[i + 1 ]:
            dp[i][state] = 1 + f(i + 1 , 1 , A, dp, N) 
        return dp[i][state]
 # Function that calls the resucrsive function to
 # fill the dp array and then returns the result
 def maxLenSeq(A, N): 
    # dp[][] array for storing result
    # of f(i, 1) and f(1, 2)
    # Populating the array dp[] with -1
    dp = [[ - 1 , - 1 , - 1 ] for i in range ( 1000 )] 
    # Make sure that longest UD and DU
    # sequence starting at each
    # index is calculated
    for i in range (N):
        tmp = f(i, 1 , A, dp, N)
        tmp = f(i, 2 , A, dp, N) 
    # Assume the answer to be -1
    # This value will only increase
    ans = - 1
    for i in range (N): 
        # y is the length of the longest
        # UD sequence starting at i
        y = dp[i][ 1 ]
        if (i + y) > = N:
            ans = max (ans, dp[i][ 1 ] + 1 ) 
        # If length is even then add an integer
        # and then a DU sequence starting at i + y
        elif y % 2 = = 0 :
            ans = max (ans, dp[i][ 1 ] + 1 + dp[i + y][ 2 ]) 
        # If length is odd then add an integer
        # and then a UD sequence starting at i + y
        elif y % 2 = = 1 :
            ans = max (ans, dp[i][ 1 ] + 1 + dp[i + y][ 1 ]) 
    return ans
 # Driver Code
 if __name__ = = "__main__" :
    A = [ 1 , 10 , 3 , 20 , 25 , 24 ]
    n = len (A)
    print (maxLenSeq(A, n))
 # This code is contributed by
 # sanjeev2552

C #

 // C# implementation of the approach
 using System;
    
class GFG
 {
    
    // Function to recursively fill the dp array
    static int f( int i, int state, int []A,
                 int [,]dp, int N)
    {
        if (i >= N)
            return 0;
    
        // If f(i, state) is already calculated
        // then return the value
        else if (dp[i, state] != -1)
        {
            return dp[i, state];
        }
    
        // Calculate f(i, state) according to the
        // recurrence relation and store in dp[,]
        else
        {
            if (i == N - 1)
                dp[i, state] = 1;
            else if (state == 1 && A[i] > A[i + 1])
                dp[i, state] = 1;
            else if (state == 2 && A[i] < A[i + 1])
                dp[i, state] = 1;
            else if (state == 1 && A[i] <= A[i + 1])
                dp[i, state] = 1 + f(i + 1, 2, A, dp, N);
            else if (state == 2 && A[i] >= A[i + 1])
                dp[i, state] = 1 + f(i + 1, 1, A, dp, N);
            return dp[i, state];
        }
    }
    
    // Function that calls the resucrsive function to
    // fill the dp array and then returns the result
    static int maxLenSeq( int []A, int N)
    {
        int i, j, tmp, y, ans;
    
        // dp[,] array for storing result
        // of f(i, 1) and f(1, 2)
        int [,]dp = new int [1000, 3];
        
        // Populating the array dp[] with -1
        for (i = 0; i < 1000; i++)
            for (j = 0; j < 3; j++)
                dp[i, j] = -1;
        // Make sure that longest UD and DU
        // sequence starting at each
        // index is calculated
        for (i = 0; i < N; i++)
        {
            tmp = f(i, 1, A, dp, N);
            tmp = f(i, 2, A, dp, N);
        }
    
        // Assume the answer to be -1
        // This value will only increase
        ans = -1;
        for (i = 0; i < N; i++)
        {
    
            // y is the length of the longest

                    
                                            Статьи
                                            Олимпиады по программированию
                                    
РЕКОМЕНДУЕМЫЕ СТАТЬИОнлайн-обменники: быстрый и удобный способ конвертации активов в современном мире
17 Апреля, 2024
Лучшие онлайн-курсы по WordPress: рейтинг 2024
29 Марта, 2024
Для кого буду полезны услуги SMS-центра
24 Марта, 2024
Что такое экспертиза исходного кода и как ее проводят?
3 Марта, 2024
Как добавить деньги на счет аккаунта Steam через криптовалюту
20 Февраля, 2024
Заказать докторскую диссертацию на заказ
30 Января, 2024
Купить лайки в ВК: зачем, сколько и где
19 Января, 2024
Как добавить деньги на свой аккаунт в Steam и начать покупать игры и контент
12 Января, 2024