Дискретная математика | Диаграммы Хассе
Диаграмма Хассе - это графическое представление отношения элементов частично упорядоченного множества (poset) с подразумеваемой ориентацией вверх . Точка рисуется для каждого элемента частично упорядоченного набора (poset) и соединяется с отрезком линии в соответствии со следующими правилами:
- Если p <q в poset, то точка, соответствующая p, отображается на чертеже ниже, чем точка, соответствующая q.
- Две точки p и q будут соединены отрезком прямой, если p связано с q .
Чтобы нарисовать диаграмму Хассе, предоставленный набор должен быть позетом.
Пусет или частично упорядоченное множество A - это пара, (B,  ) множества B, элементы которого называются вершинами A и подчиняется следующим правилам:
) множества B, элементы которого называются вершинами A и подчиняется следующим правилам:
- Рефлексивность → p
 п
п 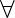 п
п 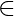 B
B - Антисимметричный → p
 q и q
q и q  p тогда и только тогда, когда p = q
p тогда и только тогда, когда p = q - Транзитивность → если p
 q и q
q и q  r, затем p
r, затем p  р
р
Пример-1: Нарисуйте диаграмму Хассе для ({3, 4, 12, 24, 48, 72}, /)
Объяснение. В соответствии с приведенным выше вопросом сначала мы должны найти посет для делимости.
Пусть набор - A.
A = {(3  12), (3
12), (3  24), (3
24), (3  48), (3
48), (3  72), (4
72), (4  12), (4
12), (4  24), (4
24), (4  48), (4
48), (4  72), (12
72), (12  24), (12
24), (12  48), (12
48), (12  72), (24
72), (24  48), (24
48), (24  72)}
72)}
Итак, теперь диаграмма Хассе будет:
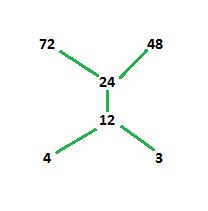
На диаграмме выше 3 и 4 находятся на одном уровне, потому что они не связаны друг с другом и меньше других элементов в наборе. Следующим последующим элементом для 3 и 4 является 12, то есть 12 делится как на 3, так и на 4. Тогда 24 делится на 3, 4 и 12. Следовательно, он помещается над 12. 24 делит как 48, так и 72, но 48 не делит. разделить 72. Следовательно, 48 и 72 не соединяются.
Мы можем видеть транзитивность на нашей диаграмме по мере увеличения уровня.
Пример-2: Нарисуйте диаграмму Хассе для (D  , /)
, /)
Пояснение - Здесь D  означает набор натуральных чисел, делителей 12.
означает набор натуральных чисел, делителей 12.
Итак, D  = {1, 2, 3, 4, 6, 12}
= {1, 2, 3, 4, 6, 12}
poset A = {(1  2), (1
2), (1  3), (1
3), (1  4), (1
4), (1  6), (1
6), (1  12), (2
12), (2  4), (2
4), (2  6), (2
6), (2  12), (3
12), (3  6), (3
6), (3  12), (4
12), (4  12), (6
12), (6  12)}
12)}
Итак, теперь диаграмма Хассе будет:
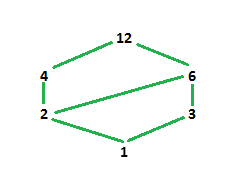
На диаграмме выше 1 - единственный элемент, который делит все остальные элементы, и самый маленький. Следовательно, он находится внизу. Тогда элементы в нашем наборе - это 2 и 3, которые не делят друг друга, поэтому они размещаются на одном уровне отдельно, но делятся на 1 (оба соединены на 1). 4 делится на 1 и 2, а 6 делится на 1, 2 и 3, следовательно, 4 соединяется на 2, а 6 соединяется на 2 и 3. 12 делится на все элементы, следовательно, на 4 и 6 соединяется не на все элементы, потому что мы уже соединили 4 и 6 с меньшими элементами соответственно.
Для обычной диаграммы Хассе:
- Максимальный элемент - это элемент POSET, который не меньше любого другого элемента POSET. Или мы можем сказать, что это элемент, не связанный ни с каким другим элементом. Верхние элементы диаграммы Хассе.
- Пример. На диаграмме выше мы можем сказать, что 4,2,3,6,1 связаны с 12 (упорядочены по делению, например (4, /)), но 12 не связаны ни с каким другим. (Поскольку диаграмма Хассе направлена вверх).
- Минимальный элемент - это элемент POSET, который не больше любого другого элемента POSET. Или мы можем сказать, что никакой другой элемент не связан с этим элементом. Нижние элементы диаграммы Хассе.
- Пример. На диаграмме выше мы можем сказать, что 1 относится к 2,3,4,6,12 (упорядочено по делению, например (4, /)), но ни один элемент не связан с 1 (поскольку диаграмма Хассе направлена вверх. ).
- Наибольший элемент (если он существует) - это элемент, следующий за всеми остальными элементами.
- Наименьший элемент - это элемент, который предшествует всем остальным элементам.
Примечание. Наибольший и наименьший элементы на диаграмме Хассе - это только один.
В Примере-1
Максимальные элементы - 48 и 72, поскольку они следуют за всеми элементами.
Минимальные элементы - 3 и 4, поскольку они предшествуют всем элементам.
Наибольший элемент не существует, поскольку нет ни одного элемента, который предшествовал бы всем элементам.
Наименьшего элемента не существует, поскольку нет ни одного элемента, предшествующего всем элементам.
В Примере-2
Максимальный и наибольший элемент - 12, а минимальный и наименьший элемент - 1.
ПРИМЕЧАНИЕ: элемент может быть как максимальным, так и минимальным.
Пример-

Здесь a, b, c максимальны, а также минимальны.