Дарт – Рекурсия

Рекурсия в любом языке программирования означает, что функция вызывает сама себя. Он используется для решения больших сложных проблем, разбивая их на более мелкие подзадачи. Dart также реализует рекурсию аналогичным образом.

В рекурсивной функции функция многократно вызывает себя, пока не будет достигнуто базовое условие. Функция в основном состоит из двух частей.

• Рекурсивный: рекурсивная часть вызывается снова и снова с меньшей подзадачей.
• База: базовое условие проверяется каждый раз при вызове функции. Если функция находится в базовом состоянии, она используется для предоставления решения.

Рекурсия использует стек для хранения значений/результатов подзадач, которые впоследствии возвращаются к основной проблеме.

Для углубленного обзора рекурсии посетите: https://www.geeksforgeeks.org/recursion/

Синтаксис:

void gfgRec()
{
    // Base code....

    gfgRec();

    // Some code...
}


void main()
{
    gfgRec();
}

Пример:

Мы будем использовать программу для n-го числа Фибоначчи, чтобы продемонстрировать рекурсию в дартс —

Выход:

8

Объяснение:

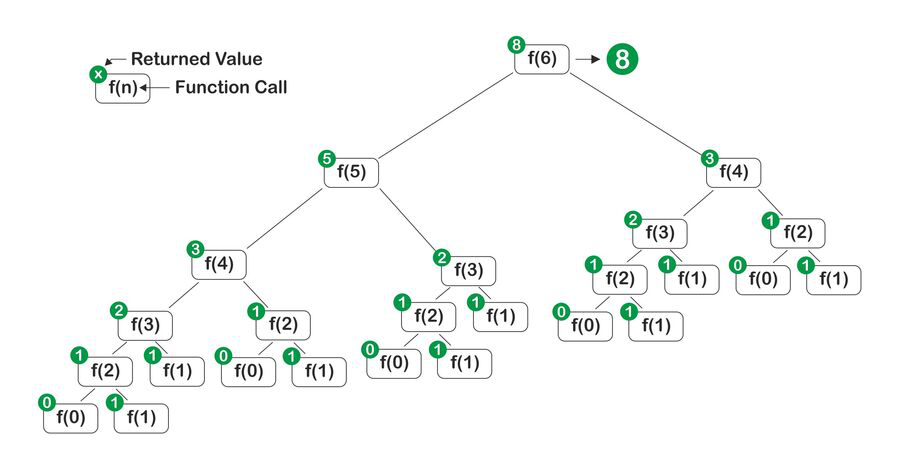
Из рисунка видно, что вызов функции с параметром n = 6, в свою очередь, вызывает сам себя с меньшими значениями 5 и 4. Они сами вызывают функцию с меньшими значениями, пока она не достигнет базового условия. Когда базовое условие выполнено, функция начинает возвращать значения. Таким образом, окончательный результат получается равным 8, что является суммой вызова 5 и 4.

В случае рекурсии проблема должна становиться меньше с каждым новым вызовом функции, поскольку проблема должна быть завершена, чтобы вернуть результат. Это условие называется условием завершения в рекурсии. В случае, если проблема не решена, это может привести к бесконечному циклу, и, как мы видим, этот вызов функции использует стековую память для хранения временных значений, они могут использовать много памяти. Если базовое условие не определено или не может быть достигнуто, функция может вызвать переполнение стека.

Некоторые преимущества и недостатки использования рекурсии

Преимущества использования рекурсии:

• Решение задачи с помощью рекурсии очень лаконичное и короткое.
• Их легко использовать с задачами, связанными с деревьями и графами.
• Снижает временную сложность задач.
• Сокращает ненужные вызовы функций.

Недостатки использования рекурсии:

• Задача занимает много места.
• Логика может быть сложной для понимания.
• При зависании трудно отлаживать.

Теперь мы будем использовать другой пример, чтобы лучше понять его реализацию в дартс.

Пример:

Мы напишем программу для нахождения факториала числа с помощью рекурсии.

Выход:

40320

Объяснение:

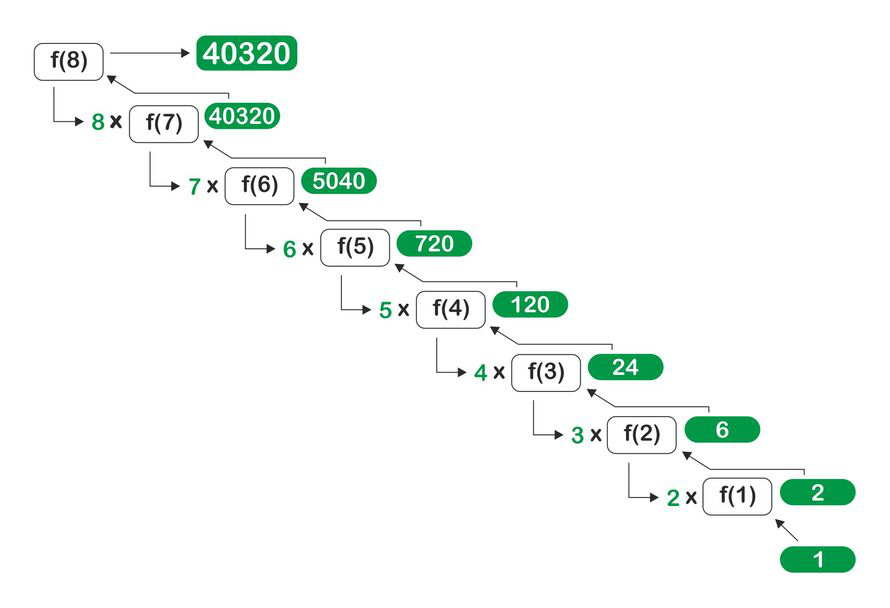
Из рисунка мы можем сделать вывод, что функция Fact вызывает себя до тех пор, пока не будет достигнуто базовое условие, т. е. мы вернули функцию с умножением значения «n» на значение функции со значением «n-1», пока не будет достигнуто значение n. становится равным 1. Наконец, мы возвращаем значение искомой функции.