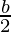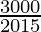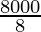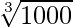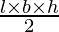Что произойдет с объемом прямоугольного параллелепипеда, если его длину увеличить в два раза, высоту оставить такой же, а ширину уменьшить вдвое?

Кубоид представляет собой трехмерный твердый объект. Его также называют правильным шестигранником, и он является одним из пяти платоновых тел. Все ребра имеют по крайней мере общее ребро друг с другом. Строение кубоида можно определить с точки зрения того факта, что каждая из граней соединяется с четырьмя вершинами и четырьмя гранями, вершина соединяется с тремя гранями и тремя гранями, а ребра соприкасаются с двумя гранями и двумя вершинами. Длина, ширина или высота могут быть или не быть равными в случае прямоугольного параллелепипеда.

Свойства прямоугольного параллелепипеда

• Все лица имеют прямоугольную форму.
• Все углы прямые
• Противоположные грани прямоугольного параллелепипеда равны.

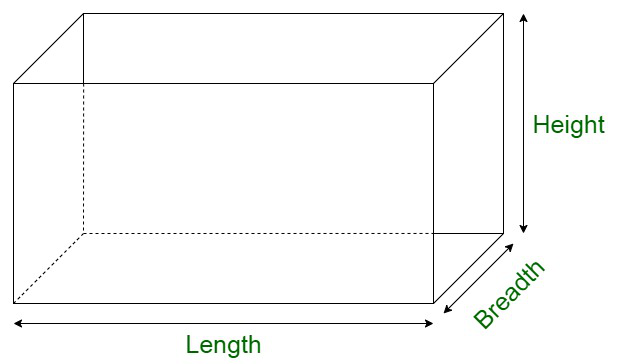
Объем прямоугольного параллелепипеда

Объем прямоугольного параллелепипеда равен объему пространства, занимаемого фигурой. Объем любой трехмерной фигуры зависит от длины трех ребер, то есть ее длины, ширины и высоты. Его можно считать сплошным прямоугольником. Примем высоту прямоугольного параллелепипеда равной h, l его длину и ширину обозначим через b единиц соответственно.

В дополнение к этому, пусть V является объемом прямоугольного параллелепипеда. Вывод его формулы,

Объем прямоугольного параллелепипеда = площадь основания × высота

Площадь основания прямоугольного параллелепипеда = l × b

Volume of a cuboid, V = l × b × h = lbh

Также,

Объем прямоугольного параллелепипеда = площадь прямоугольного параллелепипеда × высота

Что произойдет с объемом прямоугольного параллелепипеда, если его длину увеличить вдвое, а высоту оставить такой же, а ширину уменьшить вдвое?

Решение:

Let us assume l to be the length of cuboid and b to be its breadth. Also, let us assume h to be the height of the cuboid. 

So, 

Volume of a cuboid = l × b × h 

Now,  

Length of a cuboid becomes = 2l 

Breadth = b/2 

Height = h 

Volume of cuboid , on simplifying becomes, 

2l × b/2 × h 

= l × b × h 

Therefore, the final volume of the cuboid remains same. 

Примеры вопросов

Вопрос 1. Если объем прямоугольного параллелепипеда 24000 см ³ . Тогда найдите изменение объема, если его длина увеличилась вдвое, а высота осталась прежней, а ширина уменьшилась вдвое?

Решение:

Here we have to find the volume change in the cuboid if the dimensions are changed

Volume of cuboid = l × b × h = 24000 cm³

Changed dimensions

l = 2l

b = 

h = h

Therefore,

Changed dimensions volume = 2l ×  × h

Further simplifying 

Changed dimensions volume = l × b × h

Thus, we can clearly see that their is no change in the dimensions

As the dimensions are same 

Therefore,

Volume of cuboid is also same that is 24000 cm³.

Вопрос 2. Если объем прямоугольного параллелепипеда 3000 м ³ , а его длина 20 м, ширина 15 м, то найдите высоту параллелепипеда?

Решение:

Here we have to find the height of the cuboid using its volume and 2 dimensions

As we know that,

Volume of cuboid = l × b × h 

According to the question

Volume of cuboid = 3000 m³

Substituting value of volume of cuboid

3000 =  l × b × h 

3000 = 20 × 15 × h

h = 

h = 10 m

Therefore,

Height of the cuboid is 10 m.

Вопрос 3. Считайте, что длина прямоугольного параллелепипеда вдвое больше его ширины, ширина прямоугольного параллелепипеда вдвое больше его высоты , а объем прямоугольного параллелепипеда равен 8000 м ³ . Найдите все размеры прямоугольного параллелепипеда?

Решение:

Here we have to find the dimensions of the cuboid by using the given volume 8000 m³.

Assume that the height of the cuboid is ‘x’.

According to the question,

Breadth of cuboid is double its height,

So, Breadth = 2 × height = 2 × x = 2x

And, Length of cuboid is double its breadth,

So, Length = 2 × breadth = 2 × 2x = 4x

Therefore,

Length = 4x, 

Breadth = 2x

Height = x

As we know that,

Volume of cuboid = l × b × h 

Volume of cuboid = 4x × 2x × x

8000 = 8x³

x³ = 

x³ = 1000

x = 

x = 10 m

Hence,

Height of the cuboid = x = 10 m

Breadth of the cuboid = 2x = 2 × 10 = 20 m

Length of the cuboid = 4x = 4 × 10 = 40 m

Вопрос 4. Предположим, что ширина прямоугольного параллелепипеда уменьшилась вдвое. Найдите, насколько изменится объем прямоугольного параллелепипеда?

Решение:

Here we have to find the change in volume of the cuboid if its breadth is halved

As we know that

Volume of cuboid = length × breadth × height 

According to the question

The breadth is halved

So, b = 

Therefore,

Volume of cuboid = l ×  × h 

Volume of cuboid = 

Volume of cuboid = . 

Hence, 

We can see that the volume of the cuboid gets halved if its breadth gets halved.

Вопрос 5. Рассчитайте количество воды в м ³ , которое можно наполнить в резервуар для воды длиной 50 м, шириной 40 м и высотой 10 м?

Решение:

Here we have to find the amount of water that can be filled in a water tank of dimensions,

Length = 50 m

Breadth = 40 m

Height = 10 m

As we know that

Volume of cuboid = length × breadth × height 

Volume of cuboid = 50 × 40 × 10

Volume of cuboid = 20000 m³

Therefore,

20000 m³ water can be filled in the water tank.