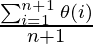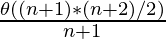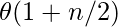Анализ алгоритмов | Большой - обозначение Θ (большое тета)

При анализе алгоритмов асимптотические обозначения используются для оценки производительности алгоритма в его лучших и худших случаях. В этой статье будут обсуждаться нотации Big – Theta, представленные греческой буквой (Θ).

Определение: Пусть g и f — функция от множества натуральных чисел к самой себе. Функция f называется Θ(g), если существуют константы c ₁ , c ₂ > 0 и натуральное число n ₀ такие, что c ₁ * g(n) ≤ f(n) ≤ c ₂ * g(n ) для всех n ≥ n ₀

Математическое представление:

Θ (g(n)) = {f(n): there exist positive constants c₁, c₂ and n₀ such that 0 ≤ c₁ * g(n) ≤ f(n) ≤ c₂ * g(n) for all n ≥ n₀}
Note: Θ(g) is a set

Приведенное выше определение означает, что если f(n) является тета g(n), то значение f(n) всегда находится между c1 * g(n) и c2 * g(n) для больших значений n (n ≥ n ₀ ). Определение тета также требует, чтобы f(n) было неотрицательным для значений n больше, чем n ₀ .

Графическое представление:

Говоря простым языком, нотация Big – Theta(Θ) задает асимптотические границы (как верхние, так и нижние) для функции f(n) и обеспечивает среднюю временную сложность алгоритма.

Выполните следующие шаги, чтобы найти среднюю временную сложность любой программы:

1. Разбейте программу на более мелкие сегменты.
2. Найдите все типы и количество входных данных и рассчитайте количество операций, которые они потребуют для выполнения. Убедитесь, что входные варианты распределены одинаково.
3. Найдите сумму всех вычисленных значений и разделите сумму на общее количество входных данных, скажем, полученная функция n равна g (n) после удаления всех констант, тогда в обозначении Θ она представлена как Θ (g (n))

Пример: Рассмотрим пример, чтобы определить, существует ли ключ в массиве или нет, используя линейный поиск. Идея состоит в том, чтобы пройтись по массиву и проверить каждый элемент, равен ли он ключу или нет.

Псевдокод выглядит следующим образом:

bool linearSearch(int a[], int n, int key)
{
    for (int i = 0; i < n; i++) {
        if (a[i] == key)
            return true;
    }

    return false;
}

Ниже приведена реализация вышеуказанного подхода:

В задаче линейного поиска предположим, что все случаи распределены равномерно (включая случай отсутствия ключа в массиве). Итак, просуммируем все случаи (когда ключ есть в позиции 1, 2, 3, ……, n и нет, и разделим сумму на n + 1.

Average case time complexity = 

⇒ 

⇒ 

⇒  (constants are removed)

Когда использовать обозначение Big – Θ: Big – Θ анализирует алгоритм с наибольшей точностью, так как при вычислении Big – Θ учитывается равномерное распределение разного типа и длины входных данных, это дает среднюю временную сложность алгоритма, которая составляет является наиболее точным при анализе, однако на практике иногда становится трудно найти равномерно распределенный набор входных данных для алгоритма, в этом случае используется нотация Big-O, которая представляет асимптотическую верхнюю границу функции f.

Для получения более подробной информации см.:
Проектирование и анализ алгоритмов.