Алгоритм пузырьковой сортировки с использованием JavaScript

Опубликовано: 18 Февраля, 2022

Алгоритм пузырьковой сортировки - это алгоритм, который сортирует массив путем сравнения двух соседних элементов и меняет их местами, если они не в намеченном порядке. Здесь порядок может быть любым, например, в порядке возрастания или убывания.

Как работает пузырьковая сортировка

У нас есть несортированный массив arr = [1, 4, 2, 5, -2, 3], задача - отсортировать массив с помощью пузырьковой сортировки.

Сортировка пузырьков сравнивает элемент из индекса 0, и если 0-й индекс меньше 1-го индекса, тогда значения меняются местами, и если 0-й индекс меньше 1-го индекса, то ничего не происходит.

затем 1-й индекс сравнивается со 2-м индексом, затем 2-й индекс сравнивается с 3-м и т. д.

давайте посмотрим на это на примере, здесь кратко проиллюстрирован каждый шаг

После каждой итерации наибольшее значение массива становится последним индексом массива. на каждой итерации сравнение происходит до последнего несортированного элемента.

Теперь сравнение сократилось на один шаг, потому что самый большой элемент находится в нужном месте.

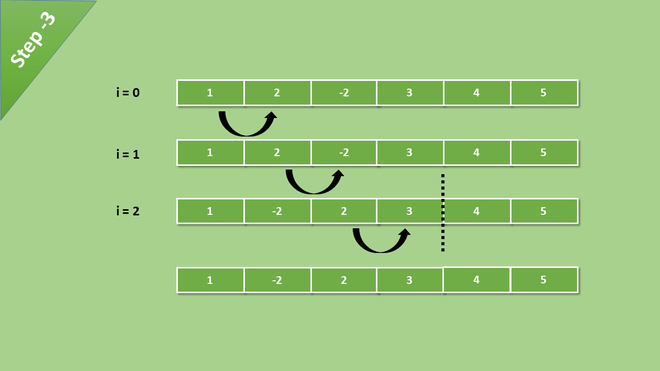
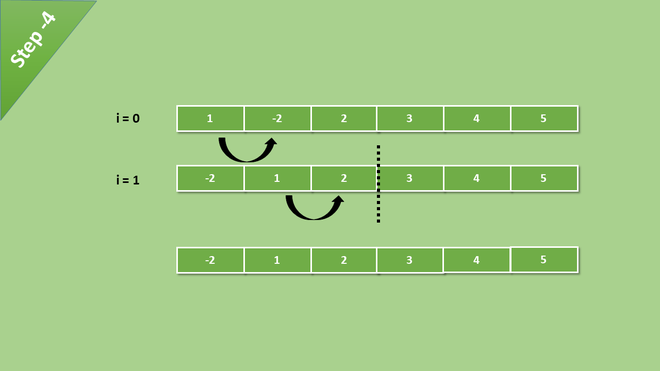
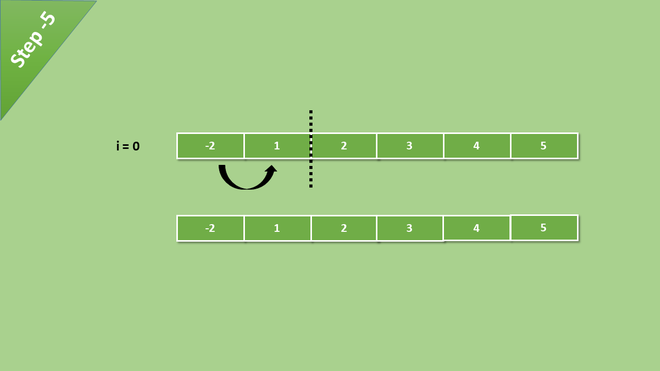
After all the iteration and comparisons of elements, we get a sorted array.

Syntax

BubbleSort(array){
  for i -> 0 to arrayLength 
     for j -> 0 to (arrayLength - i - 1)
      if arr[j] > arr[j + 1]
        swap(arr[j], arr[j + 1])
}

Implementation

Javascript

// Bubble sort Implementation using Javascript
  
  
// Creating the bblSort function
 function bblSort(arr){
     
 for(var i = 0; i < arr.length; i++){
     
   // Last i elements are already in place  
   for(var j = 0; j < ( arr.length - i -1 ); j++){
       
     // Checking if the item at present iteration 
     // is greater than the next iteration
     if(arr[j] > arr[j+1]){
         
       // If the condition is true then swap them
       var temp = arr[j]
       arr[j] = arr[j + 1]
       arr[j+1] = temp
     }
   }
 }
 // Print the sorted array
 console.log(arr);
}
  
  
// This is our unsorted array
var arr = [234, 43, 55, 63,  5, 6, 235, 547];
  
  
// Now pass this array to the bblSort() function
bblSort(arr);

Output 
Sorted array :
[5, 6, 43, 55, 63, 234, 235, 547]

Примечание: эта реализация не оптимизирована. Далее мы увидим оптимизированное решение.

Оптимизированное решение

As we discussed the implementation of bubble sort earlier that is not optimized. Even If the array is sorted, the code will run with O(n^2) complexity. Let’s see how to implement an optimized bubble sort algorithm in javascript.

The syntax for Optimized solution

BubbleSort(array){
  for i -> 0 to arrayLength 
     isSwapped <- false
     for j -> 0 to (arrayLength - i - 1)
      if arr[j] > arr[j + 1]
        swap(arr[j], arr[j + 1])
        isSwapped -> true
}

Implementation

Javascript

// Optimized implementation of bubble sort Algorithm
  
function bubbleSort(arr){
    
  var i, j;
  var len = arr.length;
    
  var isSwapped = false;
    
  for(i =0; i < len; i++){
      
    isSwapped = false;
      
    for(j = 0; j < len; j++){
        if(arr[j] > arr[j + 1]){
          var temp = arr[j]
          arr[j] = arr[j+1];
          arr[j+1] = temp;
          isSwapped = true;
        }
    }
      
    // IF no two elements were swapped by inner loop, then break 
      
    if(!isSwapped){
      break;
    }
  }
    
  // Print the array
  console.log(arr)
}
  
  
var arr = [243, 45, 23, 356, 3, 5346, 35, 5];
  
// calling the bubbleSort Function
bubbleSort(arr)

Output
Sorted Array :
[3, 5, 23, 35, 45, 243, 356, 5346]

Complexities

Worst Case and Average case time complexity

Если массив находится в обратном порядке, то это наихудший случай, и его временная сложность составляет O (n ² ).

Лучшая временная сложность случая

Если массив уже отсортирован, это лучший сценарий и его временная сложность O (n).

Вспомогательное пространство : O (1)

Misc JavaScript-Misc

Алгоритм пузырьковой сортировки с использованием JavaScript

Как работает пузырьковая сортировка

Syntax

Implementation

Javascript

Оптимизированное решение

The syntax for Optimized solution

Implementation

Javascript

Complexities

Worst Case and Average case time complexity

Лучшая временная сложность случая

РЕКОМЕНДУЕМЫЕ СТАТЬИ