2cosacosb Формула
2cosa2cosb — одна из важных тригонометрических формул, равная cos (a + b) + cos (a — b). Это одна из формул произведения на сумму, которая используется для преобразования произведения в сумму. Тригонометрия — важный раздел математики, изучающий отношения между углами и длинами сторон прямоугольных треугольников. Существует шесть тригонометрических отношений, где тригонометрическое отношение — это отношение между сторонами прямоугольного треугольника. Синус, косинус, тангенс, косеканс, секанс и котангенс — это шесть тригонометрических отношений, где функции косеканса, секанса и котангенса являются обратными функциями синуса, косинуса и тангенса соответственно.
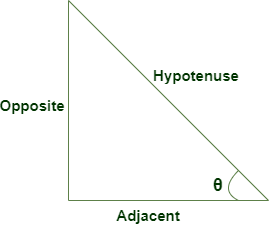
- sin θ = opposite side/hypotenuse
- cos θ = adjacent side/hypotenuse
- tan θ = opposite side/adjacent side
- cosec θ = 1/sin θ = hypotenuse/opposite side
- sec θ = 1/cos θ = hypotenuse/adjacent side
- cot θ = 1/tan θ = adjacent side/opposite side
2cosacosb Формула
2cosacosb — одна из формул произведения к сумме. Точно так же у нас есть еще три формулы произведения на сумму в тригонометрии, то есть 2sinasinb, 2sinacosb и 2cosasinb. Мы можем использовать тождество 2cosacosb для упрощения тригонометрических выражений, а также для вычисления интегралов и производных, включающих выражения вида 2cosacosb.
Формула 2cosacosb
2 Cos A cos B = cos (A+B) + cos (A-B)
Из формулы видно, что произведение двух функций косинуса преобразуется в сумму двух других функций косинуса.
Например,
Формулы произведения на сумму половинных углов:
2 cos (x/2) cos (y/2) = cos [(x + y)/2] + cos [(x – y)/2]
Вывод
From the sum and difference formulae of trigonometry, we have,
cos (A + B) = cos A cos B – sin A sin B ———— (1)
cos (A – B) = cos A cos B + sin A sin B ———— (2)
Now, by adding equations (1) and (2), we get
⇒ cos (A + B) + cos (A – B) = cos A cos B – sin A sin B + cos A cos B + sin A sin B
⇒ cos (A + B) + cos (A – B) = Cos A cos B + Cos A cos B
⇒ cos (A + B) + cos (A – B) = 2 Cos A cos B
Hence, 2 Cos A cos B = cos (A + B) + cos (A – B)
Примеры проблем
Проблема 1: Выразите 3 cos 5x cos 7x через функцию суммы.
Решение:
3 cos 5x cos 7x
Now multiply and divide the given equation by 2.
(2/2) 3 cos 5x cos 7x
= 3/2 [2 cos 5x cos 7x]
We have,
2 Cos A cos B = cos (A + B) + cos (A – B)
3/2 [2 cos 5x cos 7x] = 3/2 [cos (5x + 7x) + cos (5x – 7x)]
= 3/2 [cos (12x) + cos (-2x)]
= 3/2 [cos 12x + cos 2x] {since cos (-θ) = cos θ}
Hence, 3 cos 5x cos 7x = 3/2 [cos 12x + cos 2x]
Задача 2: Докажите, что cos 2x cos (3x/2) – cos 3x cos (5x/2) = sin x sin (9x/2).
Решение:
Let us consider the equation on left hand side,
L.H.S = cos 2x cos (3x/2) – cos 3x cos (5x/2)
= 1/2 [2 cos 2x cos (3x/2) – 2 cos 3x cos (5x/2)}
We have, 2 Cos A cos B = cos (A + B) + cos (A – B)
= 1/2 [cos (2x + 3x/2) + cos (2x – 3x/2) – cos (3x + 5x/2) – 2 cos (3x – 5x/2)]
= 1/2 [cos (7x/2) + cos (x/2) – cos (11x/2) – cos (x/2)]
= 1/2 [cos (7x/2) – cos (11x/2)]
By using cos A – cos B = – 2 sin [(A + B)/2] sin [(A – B)/2] we get,
= 1/2 {-2 sin [(7x/2 + 11x/2)/2] sin [(7x/2 – 11/2)/2]}
= – sin (18x/4) sin(-4x/4)
= – sin (9x/2) sin (-x)
= sin x sin (9x/2) {Since sin (-θ) = -sin θ}
= R.H.S
Hence, it is proved that cos 2x cos (3x/2) – cos 3x cos (5x/2) = sin x sin (9x/2)
Задача 3: Каково значение интеграла от 2 cos 4x cos (5x/2) dx?
Решение:
By,
2 cos A cos B = cos (A + B) + cos (A – B)
2 cos 4x cos (5x/2) = cos [4x + (5x/2)] + cos [4x – (5x/2)]
= cos (13x/2) + cos (3x/2)
Now, integral of 2 cos 4x cos (5x/2) dx =∫2 cos 4x cos (5x/2) dx
= ∫[cos (13x/2) + cos (3x/2)] dx
= 2/13 sin (13x/2) + 2/3 cos (3x/2) + C {Since, the integral of cos(ax) is (1/a) sin (ax) + C}
Hence, ∫ 2 cos 4x cos (5x/2) dx = (2/3) sin (3x/2) + (2/13) cos (13x/2) + C
Задача 4: Определить производную от 2 cos (x/2) cos (3x/2).
Решение:
By,
2 cos A cos B = cos (A + B) + cos (A – B)
2 cos (x/2) cos (3x/2) = cos [(x/2) + (3x/2)] + cos [(x/2) – (3x/2)]
= cos (4x/2) + cos (-2x/2)
= cos (2x) + cos (-x)
= cos x + cos 2x {since cos (-θ) = cos θ}
Now, derivative of 2 cos (x/2) cos (3x/2) = d [2 cos (x/2) cos (3x/2) ]/dx
= d [cos x + cos 2x]/dx
= – sin x – 2 sin 2x {Since, d[cos (ax)] = -a sin (ax)}
= – (sin x + sin 2x)
Hence, the derivative of 2 cos (x/2) cos (3x/2) = – (sin x + sin 2x).
Задача 5. Найдите значение выражения 3 cos 37,5° cos 52,5° по формуле 2coscosb.
Решение:
3 cos 37.5° cos 52.5° = 3/2 [2 cos 37.5° cos 52.5°]
By,
2 cos A cos B = cos (A + B) + cos (A – B)
3/2 [2 cos 37.5° cos 52.5°] = 3/2 [cos (37.5° + 52.5°) + cos (37.5° – 52.5°)]
= 3/2 [cos (90°) + cos (-12°)]
= 3/2 [cos 90° + cos 12°] {since cos (-θ) = cos θ}
cos 90° = 0 and cos 12° = 0.9781
= 3/2 [0 + 0.9781]
= 1.46715
Hence, 3 cos 37.5° cos 52.5° = 1.46715
Задача 6: Запишите 4 cos 2y cos 5y в терминах функции суммы.
Решение:
4 cos 2y cos 5y = 2 ( 2 cos 2y cos 5y)
We have,
2 Cos A cos B = cos (A + B) + cos (A – B)
2 ( 2 cos 2y cos 5y) = 2 [cos (2y + 5y) + cos (2y – 5y)]
= 2 [cos 7y + cos (-3y)]
= 2 [cos 7y + cos 3y] {since cos (-θ) = cos θ}
Hence, 4 cos 2y cos 5y = 2 [cos 7y + cos 3y]
Задача 7. Найдите значение выражения 2 cos 44,5° cos 135,5° по формуле 2coscosb.
Решение:
By,
2 cos A cos B = cos (A + B) + cos (A – B)
2 cos 44.5° cos 135.5° = cos (44.5° + 135.5°) + cos (44.5° – 135.5°)
= cos (180°) + cos (-91°)
= cos (180°) + cos (91°) {since cos (-θ) = cos θ}
= -1 + (-0.01745) = -1.01745 cos 180° = -1 and cos 91° = -0.01745
Hence, 2 cos 44.5° cos 135.5° = -1.01745