Введение в красно-черное дерево
Введение:
Красно-черное дерево — это своего рода самобалансирующееся бинарное дерево поиска, в котором каждый узел имеет дополнительный бит, и этот бит часто интерпретируется как цвет (красный или черный). Эти цвета используются для обеспечения сбалансированности дерева при вставках и удалениях. Хотя баланс дерева не идеален, он достаточно хорош, чтобы сократить время поиска и поддерживать его около времени O(log n), где n — общее количество элементов в дереве. Это дерево было изобретено в 1972 году Рудольфом Байером.
Следует отметить, что, поскольку каждому узлу требуется только 1 бит пространства для хранения информации о цвете, эти типы деревьев занимают такое же место в памяти, что и классическое (неокрашенное) двоичное дерево поиска.
Правила, которым следует каждое красно-черное дерево:
- Каждый узел имеет красный или черный цвет.
- Корень дерева всегда черный.
- Нет двух соседних красных узлов (красный узел не может иметь красного родителя или красного дочернего элемента).
- Каждый путь от узла (включая корень) к любому из его потомков NULL узлов имеет одинаковое количество черных узлов.
- Все листовые узлы являются черными узлами.
Почему красно-черные деревья?
Большинство операций BST (например, поиск, макс, минимум, вставка, удаление и т. д.) занимают время O(h), где h — высота BST. Стоимость этих операций может стать O (n) для искаженного двоичного дерева. Если мы убедимся, что высота дерева остается O(log n) после каждой вставки и удаления, то мы можем гарантировать верхнюю границу O(log n) для всех этих операций. Высота красно-черного дерева всегда равна O(log n), где n — количество узлов в дереве.
| Старший Нет. | Алгоритм | Сложность времени |
|---|---|---|
| 1. | Поиск | О (журнал п) |
| 2. | Вставлять | О (журнал п) |
| 3. | Удалить | О (журнал п) |
«n» — общее количество элементов в красно-черном дереве.
Сравнение с деревом AVL:
Деревья AVL более сбалансированы по сравнению с красно-черными деревьями, но они могут вызывать больше поворотов при вставке и удалении. Поэтому, если ваше приложение предполагает частые вставки и удаления, предпочтение следует отдавать красно-черным деревьям. А если вставки и удаления происходят реже, а поиск — более частая операция, то дерево AVL следует предпочесть красно-черному дереву.
Как красно-черное дерево обеспечивает баланс?
Простой пример для понимания балансировки: цепочка из 3 узлов невозможна в красно-черном дереве. Мы можем попробовать любую комбинацию цветов и посмотреть, все ли они нарушают свойство красно-черного дерева.
Интересные моменты о красно-черном дереве:
- Черная высота красно-черного дерева — это количество черных узлов на пути от корневого узла до листового узла. Листовые узлы также считаются черными узлами. Итак, красно-черное дерево высоты h имеет высоту черного >= h/2.
- Высота красно-черного дерева с n узлами равна h<= 2 log 2 (n + 1).
- Все листья (NIL) черные.
- Глубина черного узла определяется как количество черных узлов от корня до этого узла, т. е. количество черных предков.
- Каждое красно-черное дерево является частным случаем бинарного дерева.
Черный Высота красно-черного дерева:
Высота черного — это количество черных узлов на пути от корня к листу. Листовые узлы также считаются черными узлами. Из приведенных выше свойств 3 и 4 мы можем вывести, что Красно-черное дерево высоты h имеет высоту черного >= h/2 .
Number of nodes from a node to its farthest descendant leaf is no more than twice as the number of nodes to the nearest descendant leaf.
Каждое красное черное дерево с n узлами имеет высоту <= 2Log 2 (n+1)
Это можно доказать с помощью следующих фактов:
- Для общего двоичного дерева пусть k будет минимальным количеством узлов на всех путях от корня до NULL, тогда n >= 2 k – 1 (например, если k равно 3, то n равно как минимум 7). Это выражение также можно записать как k <= Log 2 (n+1).
- Из свойства 4 красно-черных деревьев и утверждения выше мы можем сказать, что в красно-черном дереве с n узлами существует путь от корня к листу с не более чем Log 2 (n + 1) черными узлами.
- Из свойств 3 и 5 красно-черных деревьев мы можем утверждать, что количество черных узлов в красно-черном дереве не менее ⌊ n/2 ⌋, где n — общее количество узлов.
Из вышеизложенного можно сделать вывод, что Красное Черное Дерево с n узлами имеет высоту <= 2Log 2 (n+1)
Операция поиска в красно-черном дереве:
Поскольку каждое красно-черное дерево является частным случаем бинарного дерева, алгоритм поиска красно-черного дерева аналогичен алгоритму поиска бинарного дерева.
Алгоритм:
searchElement (tree, val)
Step 1:
If tree -> data = val OR tree = NULL
Return tree
Else
If val < data
Return searchElement (tree -> left, val)
Else
Return searchElement (tree -> right, val)
[ End of if ]
[ End of if ]
Step 2: ENDЧто касается программы, вы можете обратиться к дереву AVL.
Пример: Поиск 11 в следующем красно-черном дереве.
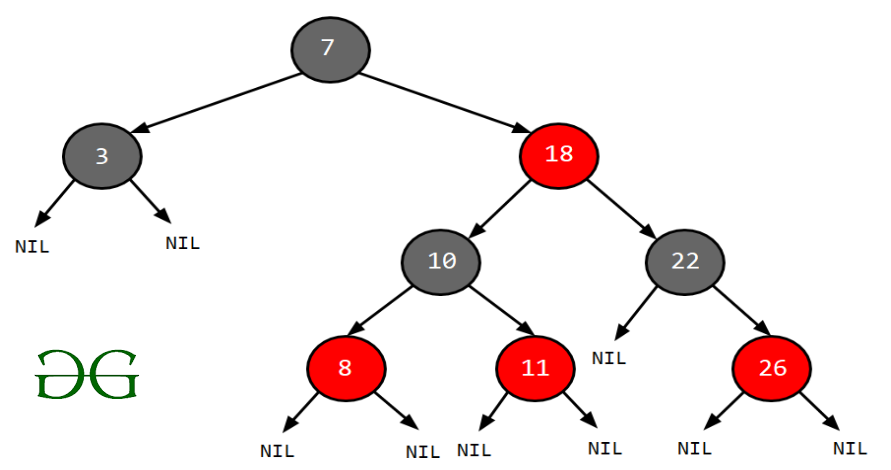
Решение:
- Начните с корня.
- Сравните вставляемый элемент с корнем, если меньше, чем корень, то рекурсивно для левого, иначе рекурсивно для правого.
- Если элемент для поиска найден где угодно, верните true, иначе верните false.
В этом посте мы представили красно-черные деревья и обсудили, как обеспечивается баланс. Сложность заключается в поддержании баланса при добавлении и удалении ключей. Мы также видели, как искать элемент в красно-черном дереве. Вскоре мы обсудим операции вставки и удаления в следующих сообщениях о красно-черном дереве.
Упражнение:
1) Возможно ли иметь все черные узлы в красно-черном дереве?
2) Нарисовать красно-черное дерево, которое не является деревом AVL по структуре?
Вставка и удаление
Вставка красно-черного дерева
Удаление красно-черного дерева
Приложения:
- Большинство самобалансирующихся библиотечных функций BST, таких как map, multiset и multimap в C++ (или пакеты Java, такие как java.util.TreeMap и java.util.TreeSet), используют красно-черные деревья.
- Он используется для реализации CPU Scheduling Linux. Полностью Fair Scheduler использует его.
- Он также используется в алгоритме кластеризации K-mean в машинном обучении для уменьшения временной сложности.
- Кроме того, MySQL также использует красно-черное дерево для индексов таблиц, чтобы сократить время поиска и вставки.
Использованная литература:
- Введение в алгоритмы, 3-е издание Клиффорда Штейна, Томаса Х. Кормена, Чарльза Э. Лейзерсона, Рональда Л. Ривеста.
- http://en.wikipedia.org/wiki/Red%E2%80%93black_tree
- Видеолекция Тима Рафгардена о красно-черном дереве
- Видеолекция Массачусетского технологического института о красно-черном дереве
- Конспект лекций Массачусетского технологического института о красно-черном дереве