Введение в грамматику в теории вычислений
Предварительное условие - теория вычислений
Грамматика:
Это конечный набор формальных правил для создания синтаксически правильных предложений или содержательных правильных предложений.
Составить грамматику:
Грамматика в основном состоит из двух основных элементов:
- Символы клемм -
Терминальные символы - это те, которые являются компонентами предложений, сгенерированных с использованием грамматики, и представлены строчной буквой, такой как a, b, c и т. Д. - Нетерминальные символы -
Нетерминальные символы - это те символы, которые участвуют в генерации предложения, но не являются его составной частью. Нетерминальные символы также называются вспомогательными символами и переменными. Эти символы представлены заглавными буквами, например A, B, C и т. Д.
Формальное определение грамматики:
Любая грамматика может быть представлена 4 кортежами - <N, T, P, S>
- N - конечный непустой набор нетерминальных символов.
- T - конечный набор терминальных символов.
- P - конечный непустой набор производственных правил.
- S - Начальный символ (символ, с которого мы начинаем создавать наши предложения или строки).
Правила производства:
Производственное или производственное правило в информатике - это правило перезаписи, определяющее замену символов, которая может выполняться рекурсивно для генерации новых последовательностей символов. Это имеет вид 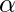 ->
-> 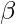 куда
куда 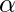 - нетерминальный символ, который можно заменить на
- нетерминальный символ, который можно заменить на 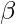 который представляет собой строку терминальных символов или нетерминальных символов.
который представляет собой строку терминальных символов или нетерминальных символов.
Пример-1:
Рассмотрим грамматику G1 = <N, T, P, S>
T = {a, b} # Набор терминальных символов
P = {A-> Aa, A-> Ab, A-> a, A-> b, A-> 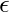 } # Набор всех производственных правил
S = {A} # Символ начала
} # Набор всех производственных правил
S = {A} # Символ началаПоскольку начальным символом является S, мы можем получить Aa, Ab, a, b, 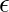 который может также создавать строки, в которых A может быть заменен на строки, упомянутые в правилах производства, и, следовательно, эта грамматика может использоваться для создания строк формы (a + b) *.
который может также создавать строки, в которых A может быть заменен на строки, упомянутые в правилах производства, и, следовательно, эта грамматика может использоваться для создания строк формы (a + b) *.
Вывод строк:
A-> a # using production rule 3 ИЛИ A-> Aa # using production rule 1 Aa-> ba # using производственное правило 4 ИЛИ A-> Aa # using production rule 1 Aa-> AAa # using production rule 1 AAa-> bAa # using продукционное правило 4 bAa-> ba # using производственное правило 5
Пример-2:
Рассмотрим грамматику G2 = <N, T, P, S>
N = {A} # Набор нетерминальных символов
T = {a} # Набор терминальных символов
P = {A-> Aa, A-> AAa, A-> a, A-> 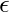 } # Набор всех производственных правил
S = {A} # Символ начала
} # Набор всех производственных правил
S = {A} # Символ началаПоскольку начальным символом является S, мы можем получить Aa, AAa, a,  который может также создавать строки, в которых A может быть заменен на строки, упомянутые в правилах производства, и, следовательно, эта грамматика может использоваться для создания строк формы (a) *.
который может также создавать строки, в которых A может быть заменен на строки, упомянутые в правилах производства, и, следовательно, эта грамматика может использоваться для создания строк формы (a) *.
Вывод строк:
A-> a # using production rule 3 ИЛИ A-> Aa # using production rule 1 Aa-> aa # using production rule 3 ИЛИ A-> Aa # using production rule 1 Aa-> AAa # using production rule 1 AAa-> Aa # using production rule 4 Aa-> aa # using production rule 3
Эквивалентные грамматики:
Грамматики считаются эквивалентными, т. Е. Они производят один и тот же язык.
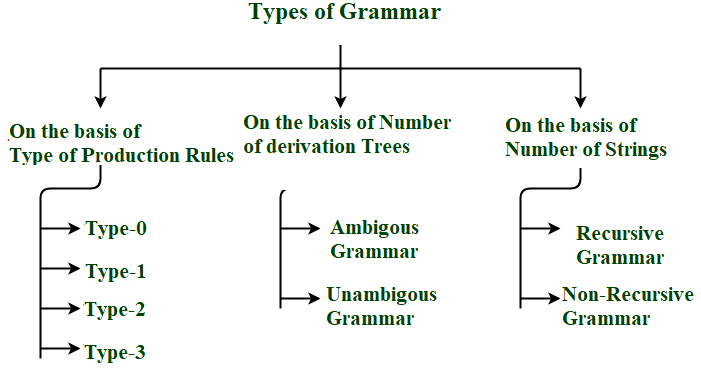
Различные типы грамматик:
Грамматику можно разделить на:
- Тип правил производства
- Количество деревьев деривации
- Количество струн