Вставка в красно-черное дерево

В предыдущем посте мы обсуждали введение в Red-Black Trees. В этом посте обсуждается вставка. При вставке дерева AVL мы использовали вращение как инструмент для балансировки после вставки. В красно-черном дереве мы используем два инструмента для балансировки.

1. Перекрашивание
2. Вращение

Перекрашивание — это изменение цвета узла, т. е. если он красный, то измените его на черный и наоборот. Следует отметить, что цвет узла NULL всегда черный. Более того, мы всегда сначала пытаемся перекраситься, если перекрасить не получается, то идем на ротацию. Ниже приведен подробный алгоритм. Алгоритмы имеют в основном два случая в зависимости от цвета дяди. Если дядя красный, мы перекрашиваем. Если дядя черный, мы делаем повороты и/или перекрашиваем.

Представление, с которым мы будем работать:

Логика:

Во-первых, вы должны вставить узел аналогично узлу в двоичном дереве и присвоить ему красный цвет. Теперь, если узел является корневым узлом, измените его цвет на черный, но если это не так, проверьте цвет родительского узла. Если его цвет черный, не меняйте цвет, но если это не так, то есть красный, проверьте цвет дяди узла. Если дядя узла имеет красный цвет, измените цвет родителя и дяди узла на черный, а цвет дедушки на красный и повторите тот же процесс для него (т.е. дедушки). Если дедушка является корнем, не меняйте дедушку на красный цвет.

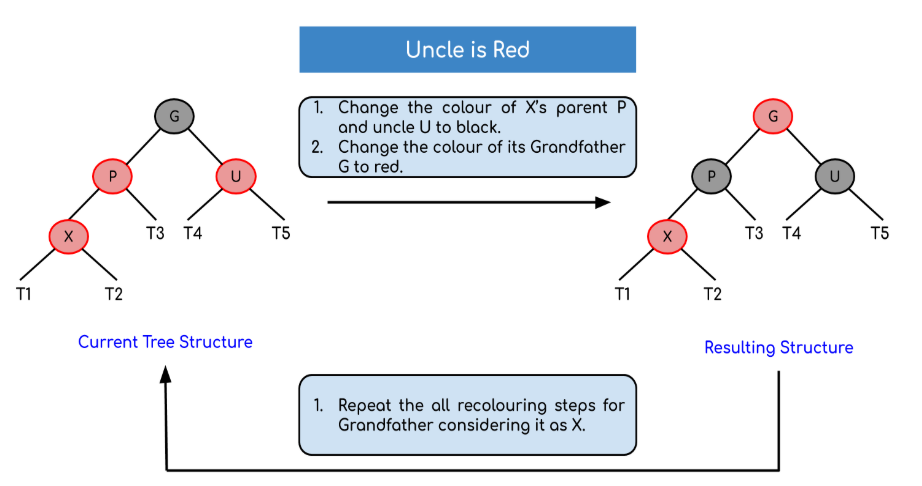
Но, если дядя узла имеет черный цвет, то возможны 4 случая:

• Левый левый корпус (вращение LL):

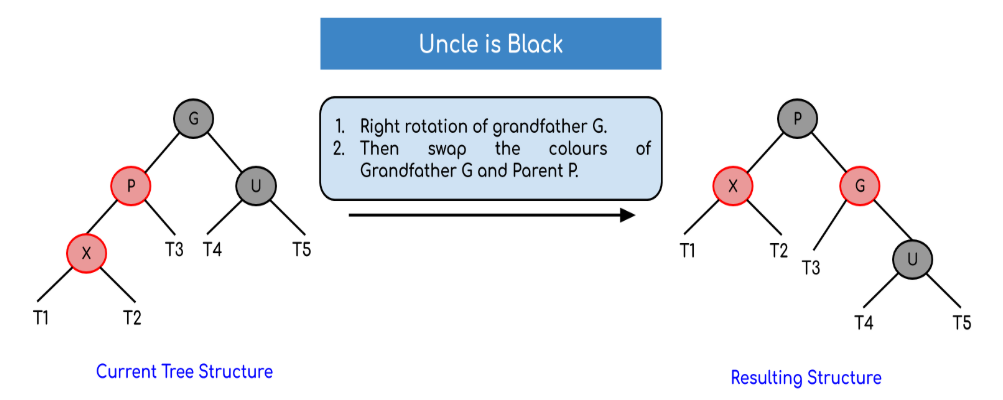
• Левый правый корпус (вращение LR):

• Правый правый корпус (вращение RR):

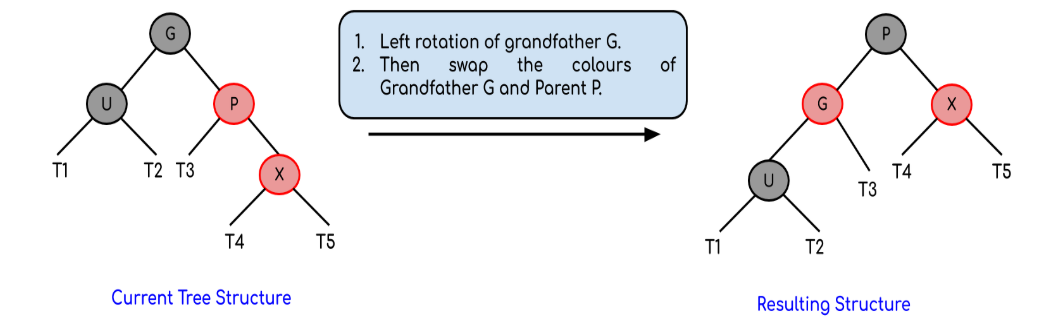
• Правый левый корпус (вращение RL):

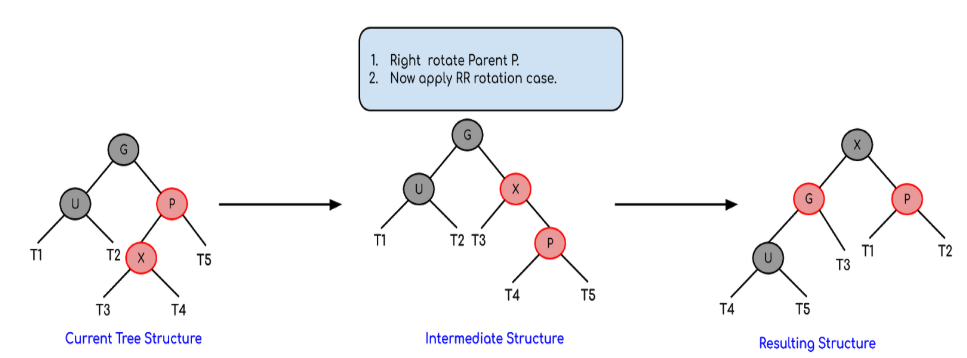
Теперь, после этих поворотов, перекрасьте в соответствии с случаем поворота (подробности см. В алгоритме).

Алгоритм:

Пусть x будет вновь вставленным узлом.

1. Выполните стандартную вставку BST и сделайте цвет вновь вставленных узлов КРАСНЫМ.
2. Если x является корнем, измените цвет x на ЧЕРНЫЙ (высота черного всего дерева увеличивается на 1).
3. Сделайте следующее, если цвет родителя x не ЧЕРНЫЙ и x не является корнем.
   а) Если дядя x КРАСНЫЙ (дедушка должен быть черным из свойства 4)
   (i) Измените цвет родителя и дяди на ЧЕРНЫЙ.
   (ii) Цвет дедушки и бабушки как КРАСНЫЙ.
   (iii) Измените x = прародитель x, повторите шаги 2 и 3 для нового x.
   б) Если дядя x является BLACK , то может быть четыре конфигурации для x, родитель x ( p ) и дедушка и дедушка x ( g ) (это похоже на AVL Tree)
   (i) Левый левый случай (p — левый дочерний элемент g, а x — левый дочерний элемент p)
   (ii) Лево-правый случай (p — левый дочерний элемент g, а x — правый дочерний элемент p)
   (iii) Правильный правильный случай (Зеркало случая i)
   (iv) Правый левый случай (Зеркало случая ii)

Перекрашивание после поворотов :
Для левого левого случая [3.b (i)] и правого и правого случая [3.b (iii)] поменять местами цвета дедушки и бабушки и родителя после вращения
Для левого и правого случая [3.b (ii)] и правого и левого случая [3.b (iv)] поменяйте местами цвета прародителя и вставленного узла после вращения

Пример: Создание красно-черного дерева с элементами 3, 21, 32 и 15 в пустом дереве.

Решение:

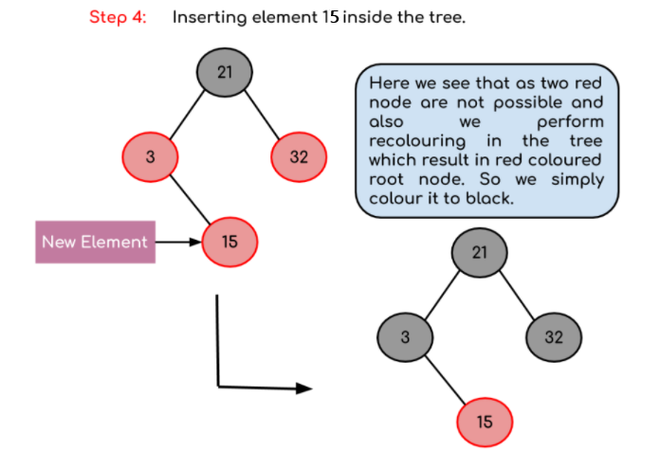
Окончательная структура дерева:

Пожалуйста, обратитесь к программе C для вставки красного черного дерева для полной реализации вышеописанного алгоритма.

Красно-черное дерево | Набор 3 (Удалить)

Код для вставки в Java.

Вот код, написанный на java для реализации RED-BLACK Trees

Следующий код также реализует вставку и обход дерева.

в конце вы также можете визуализировать построенное дерево!!!.