Вертикальный обход двоичного дерева с использованием карты
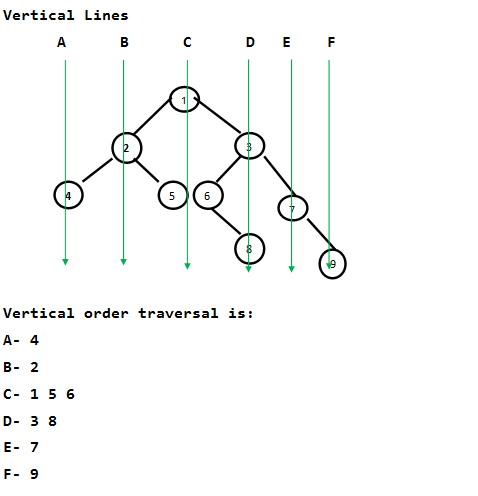
Имея бинарное дерево, выведите его вертикально. Следующие примеры иллюстрируют обход вертикального порядка.
Примеры:
Input: 1
/
2 3
/ /
4 5 6 7
/
8 9Output:
4
2
1 5 6
3 8
7
9
Вертикальный обход бинарного дерева с использованием хеширования :
Чтобы решить проблему, следуйте следующей идее:
We need to check the Horizontal Distances from the root for all nodes. If two nodes have the same Horizontal Distance (HD), then they are on the same vertical line. The idea of HD is simple. HD for root is 0, a right edge (edge connecting to right subtree) is considered as +1 horizontal distance and a left edge is considered as -1 horizontal distance.
Выполните следующие шаги, чтобы решить проблему:
- Выполните предварительный обход заданного двоичного дерева.
- Обходя дерево, мы можем рекурсивно вычислить HD. Сначала мы передаем горизонтальное расстояние как 0 для корня.
- Для левого поддерева мы передаем горизонтальное расстояние как горизонтальное расстояние от корня минус 1.
- Для правого поддерева мы передаем горизонтальное расстояние как горизонтальное расстояние корня плюс 1.
- Для каждого значения HD мы поддерживаем список узлов в хэш-карте. Всякий раз, когда мы видим узел в обходе, мы переходим к записи хеш-карты и добавляем узел в хэш-карту, используя HD в качестве ключа в карте.
Ниже приведена реализация вышеуказанного подхода, спасибо Chirag за предоставление приведенной ниже реализации C++:
Временная сложность: O (N log N). Решение на основе хеширования можно рассматривать как O(N) при условии, что у нас есть хорошая хэш-функция, которая позволяет выполнять операции вставки и извлечения за время O(1). В приведенной выше реализации C++ используется карта STL. map в STL обычно реализуется с использованием самобалансирующегося двоичного дерева поиска, где все операции занимают время O (Log N).
Вспомогательное пространство: O(N)
Примечание. Приведенное выше решение может не печатать узлы в том же вертикальном порядке, в котором они отображаются в дереве.
Например, приведенная выше программа печатает 12 вместо 9. См. здесь пример запуска.
1
/
2 3
/ /
4 5 6 7
/
8 9
/
10 11
12
Обратитесь к сообщению ниже для решения на основе обхода порядка уровней. Сообщение ниже гарантирует, что узлы вертикальной линии печатаются в том же порядке, в котором они появляются в дереве: Печать двоичного дерева в вертикальном порядке | Набор 3 (с использованием обхода порядка уровней)
Вывести обход бинарного дерева по вертикали в том же порядке, в котором они появляются:
Чтобы решить проблему, следуйте следующей идее:
We can also maintain the order of nodes in the same vertical order as they appear in the tree. Nodes having the same horizontal distance will print according to level order.
For example, In below diagram 9 and 12 have the same horizontal distance. We can make sure that if a node like 12 comes below in the same vertical line, it is printed after a node like 9Idea: Instead of using horizontal distance as a key in the map, we will use horizontal distance + vertical distance as the key. We know that the number of nodes can’t be more than the integer range in a binary tree.
We will use the first 30 bits of the key for horizontal distance [MSB to LSB] and will use the 30 next bits for vertical distance. Thus keys will be stored in the map as per our requirement.
Выполните следующие шаги, чтобы решить проблему:
- Объявить карту для хранения значения узлов на каждом уровне
- Если корень равен нулю, вернитесь из функции (базовый случай)
- Создайте целочисленное значение и установите его значение на расстояние по горизонтали << 30 ИЛИ расстояние по вертикали.
- Вставьте root->data в карту, используя val в качестве ключа
- Повторять для root->left и root->right с расстоянием по горизонтали – 1, расстоянием по вертикали + 1 и расстоянием по горизонтали + 1, расстоянием по вертикали -1 соответственно
- Распечатайте решение, используя карту
Ниже приведена реализация вышеуказанного подхода:
Временная сложность: O (N Log N)
Вспомогательное пространство: O(N)
Вертикальный обход бинарного дерева с использованием метода calculateIfAbsent в Java:
Мы можем написать код более лаконично, используя метод calculateIfAbsent карты в java и используя древовидную карту для естественной сортировки на основе ключей.
Ниже приведена реализация вышеуказанного подхода:
Временная сложность: O (N Log N)
Вспомогательное пространство: O(N)
Вертикальный обход бинарного дерева с использованием метода неупорядоченной карты:
Примечание. Мы видели упорядоченную карту выше, но ее сложность составляет O (N log N), а также она не печатает вертикальные узлы одного и того же горизонтального расстояния в правильном порядке.
Here we implement this using an unordered map, as the unordered map is implemented using a hash table its complexity is O(n), better than using an ordered map which is implemented using a BST.
Выполните следующие шаги, чтобы решить проблему:
- Создайте очередь пары для хранения узла и его горизонтального расстояния в дереве.
- Создайте карту для хранения значения узлов на каждом горизонтальном расстоянии
- Теперь выполните BFS на дереве
- На каждой итерации сохраняйте узлы с определенным горизонтальным расстоянием на карте.
- Поместите в очередь левый и правый дочерние элементы дерева с расстоянием по горизонтали - 1 и расстоянием по горизонтали + 1.
- Распечатайте ответ, используя карту
Примечание. Здесь для печати всех узлов с одинаковым горизонтальным расстоянием от корня мы используем две переменные mn и mx, которые хранят минимальное и максимальное горизонтальное расстояние от корня:
Временная сложность: O(N)
Вспомогательное пространство: O(N)