Трехмерное построение в Python с использованием Matplotlib
Matplotlib был введен с учетом только двухмерного построения графиков. Но в то время, когда вышел релиз 1.0, 3D-утилиты были разработаны на основе 2D, и, таким образом, у нас есть 3D-реализация данных, доступная сегодня! Трехмерные графики активируются путем импорта набора инструментов mplot3d. В этой статье мы разберемся с трехмерными графиками с помощью matplotlib.
Example:
import numpy as npimport matplotlib.pyplot as plt fig = plt.figure()ax = plt.axes(projection ="3d") |
Выход:
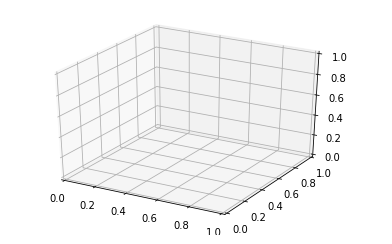
С указанным выше синтаксисом задействованы трехмерные оси, и данные могут быть нанесены на график в трех измерениях. Трехмерный график дает динамический подход и делает данные более интерактивными. Как и в случае с двумерными графиками, мы можем использовать разные способы представления трехмерных графиков. Мы можем сделать точечный график, контурный график, поверхностный график и т. Д. Давайте посмотрим на различные трехмерные графики.
Построение трехмерных линий и точек
График с линиями и точками - это простейший трехмерный график. ax.plot3d и ax.scatter - это функции для построения линейного и точечного графиков соответственно.
Example 1: 3 dimensional line graph
# importing mplot3d toolkits, numpy and matplotlibfrom mpl_toolkits import mplot3dimport numpy as npimport matplotlib.pyplot as plt fig = plt.figure() # syntax for 3-D projectionax = plt.axes(projection ="3d") # defining all 3 axesz = np.linspace(0, 1, 100)x = z * np.sin(25 * z)y = z * np.cos(25 * z) # plottingax.plot3D(x, y, z, "green")ax.set_title("3D line plot geeks for geeks")plt.show() |
Выход:
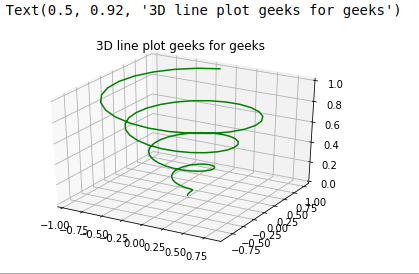
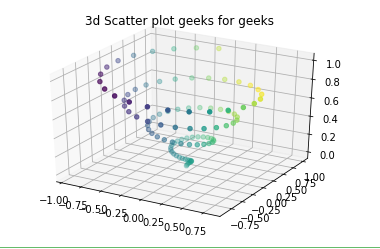
Example 2: 3 dimensional scattered graph
# importing mplot3d toolkitsfrom mpl_toolkits import mplot3dimport numpy as npimport matplotlib.pyplot as plt fig = plt.figure() # syntax for 3-D projectionax = plt.axes(projection ="3d") # defining axesz = np.linspace(0, 1, 100)x = z * np.sin(25 * z)y = z * np.cos(25 * z)c = x + yax.scatter(x, y, z, c = c) # syntax for plottingax.set_title("3d Scatter plot geeks for geeks")plt.show() |
Выход:
Построение поверхностных графиков и каркасов
Поверхностный график и каркасный график работают с данными с координатной сеткой. Они берут значение сетки и наносят его на трехмерную поверхность.
Example 1: Surface graph
# importing librariesfrom mpl_toolkits import mplot3dimport numpy as npimport matplotlib.pyplot as plt # defining surface and axesx = np.outer(np.linspace(-2, 2, 10), np.ones(10))y = x.copy().Tz = np.cos(x ** 2 + y ** 3) fig = plt.figure() # syntax for 3-D plottingax = plt.axes(projection ="3d") # syntax for plottingax.plot_surface(x, y, z, cmap ="viridis", edgecolor ="green")ax.set_title("Surface plot geeks for geeks")plt.show() |
Выход:
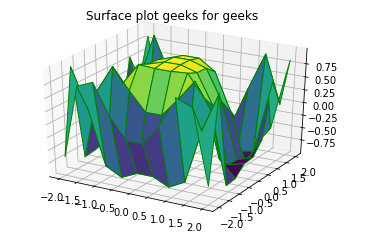
Example 2: Wireframes
from mpl_toolkits import mplot3dimport numpy as npimport matplotlib.pyplot as plt # function for z axeadef f(x, y): return np.sin(np.sqrt(x ** 2 + y ** 2)) # x and y axisx = np.linspace(-1, 5, 10)y = np.linspace(-1, 5, 10) X, Y = np.meshgrid(x, y)Z = f(X, Y) fig = plt.figure()ax = plt.axes(projection ="3d")ax.plot_wireframe(X, Y, Z, color ="green")ax.set_title("wireframe geeks for geeks"); |
Выход:

Построение контурных графиков
Контурный график принимает все входные данные в виде двумерных регулярных сеток, а данные Z оцениваются в каждой точке. Мы используем функцию ax.contour3D для построения контурного графика.
Example:
from mpl_toolkits import mplot3dimport numpy as npimport matplotlib.pyplot as plt # function for z axisdef f(x, y): return np.sin(np.sqrt(x ** 2 + y ** 3)) # x and y axisx = np.linspace(-1, 5, 10)y = np.linspace(-1, 5, 10)X, Y = np.meshgrid(x, y)Z = f(X, Y) fig = plt.figure()ax = plt.axes(projection ="3d") # ax.contour3D is used plot a contour graphax.contour3D(X, Y, Z) |
Выход:
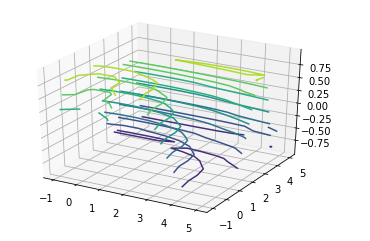
Построение триангуляции поверхности
Приведенный выше график иногда слишком ограничен и неудобен. Таким образом, мы используем набор случайных розыгрышей. Функция ax.plot_trisurf используется для построения этого графика. Это не так ясно, но более гибко.
Example:
from mpl_toolkits import mplot3dimport numpy as npimport matplotlib.pyplot as plt # angle and radiustheta = 2 * np.pi * np.random.random(100)r = 6 * np.random.random(100) # all three axesx = np.ravel(r * np.sin(theta))y = np.ravel(r * np.cos(theta))z = f(x, y) ax = plt.axes(projection ="3d")ax.scatter(x, y, z, c = z, cmap ="viridis", linewidth = 0.25); ax = plt.axes(projection ="3d")ax.plot_trisurf(x, y, z, cmap ="viridis", edgecolor ="green"); |
Выход:
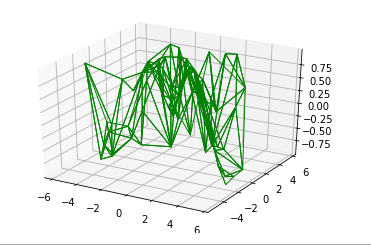
Построение ленты Мебиуса
Лента Мебиуса, также называемая скрученным цилиндром, представляет собой одностороннюю поверхность без границ. Чтобы создать ленту Мебиуса, подумайте о ее параметризации, это двухмерная полоса, и нам нужны два внутренних измерения. Диапазон углов от 0 до 2 кругов вокруг петли и ширина от -1 до 1.
Example:
from mpl_toolkits import mplot3dimport numpy as npimport matplotlib.pyplot as pltfrom matplotlib.tri import Triangulation theta = np.linspace(0, 2 * np.pi, 10)w = np.linspace(-1, 5, 8)w, theta = np.meshgrid(w, theta)phi = 0.5 * theta # radius in x-y planer = 1 + w * np.cos(phi) # all three axesx = np.ravel(r * np.cos(theta))y = np.ravel(r * np.sin(theta))z = np.ravel(w * np.sin(phi)) # triangulate in the underlying # parametrizationtri = Triangulation(np.ravel(w), np.ravel(theta)) ax = plt.axes(projection ="3d")ax.plot_trisurf(x, y, z, triangles = tri.triangles, cmap ="viridis", linewidths = 0.2); |
Выход:

Внимание компьютерщик! Укрепите свои основы с помощью базового курса программирования Python и изучите основы.
Для начала подготовьтесь к собеседованию. Расширьте свои концепции структур данных с помощью курса Python DS. А чтобы начать свое путешествие по машинному обучению, присоединяйтесь к курсу Машинное обучение - базовый уровень.