Тождество Безу (лемма Безу)

Пусть и б - любое целое число, а g - его наибольший общий делитель a и b . Тогда существуют целые числа x и y такие, что ax + by = g… (1) .

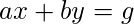
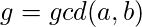
Пара (x, y), удовлетворяющая приведенному выше уравнению, не единственна. Однако все возможные решения можно просчитать.

Мы можем найти x ' и y ', который удовлетворяет (1) с использованием алгоритмов Евклида. Все возможные решения (1) даются формулами,

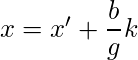
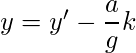
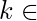
где k - любое целое число.

Легко понять, почему это так. Просто подключите решения к (1), чтобы получить интуицию.

Также важно видеть, что для общего уравнения вида

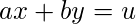
u = gcd (a, b) - наименьшее положительное целое число, для которого ax + by = u имеет решение с целыми значениями x и y .

Statement:  If gcd(a, c)=1 and gcd(b, c)=1, then gcd(ab, c)=1.

Proof: 

Above can be easily proved using Bezout’s Identity.

ax+cy=1 and bu+cv=1

Multiply the above two equations,

(ax+cy)(bu+cv)=1

The above implies,

ab(ux)+c(axv+buy+cyv)=1

1 is the only integer dividing L.H.S and R.H.S .

Hence, gcd(ab, c) = 1.

Ссылка:

https://brilliant.org/wiki/bezouts-identity/

https://en.wikipedia.org/wiki/B%C3%A9zout%27s_identity

Вниманию читателя! Не переставай учиться сейчас. Ознакомьтесь со всеми важными концепциями теории CS для собеседований по SDE с помощью курса теории CS по доступной для студентов цене и будьте готовы к работе в отрасли.