Таблица Кэли и циклическая группа | Математика

Стол Кэли -

Если G - конечная группа с операцией * , таблица Кэли группы G - это таблица со строками и столбцами, помеченными элементами группы. Запись в строке с меткой и столбец с меткой его элемент g * h.

Пример: давайте построим таблицу Кэли группы Z ₅ , целые числа {0, 1, 2, 3, 4} по модулю сложения 5.

Шаг №1: Мы обозначим строки и столбцы элементами Z ₅ в том же порядке слева направо и сверху вниз.
Шаг №2: Заполним таблицу. Каждая запись является результатом добавления метки строки к метке столбца с последующим уменьшением мода 5.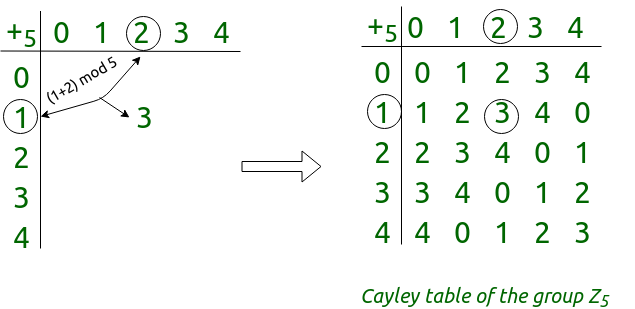

Особенности стола Кэли -
• Каждая строка и столбец таблицы должны содержать каждый элемент ровно один раз. Если таблица не имеет этого свойства, она не может представлять группу; Закон об отмене не действует.
• Идентификационный элемент группы должен не только появляться в каждой строке и столбце (ровно один раз), но он также должен быть «симметрично распределен» относительно главной диагонали. В противном случае один или несколько элементов в таблице не имеют инверсии.
• В таблице не должно быть записей, не являющихся меткой строки / столбца. В противном случае операция не закрывается.
• Должна быть одна строка, в которой названия столбцов располагаются по порядку, это указывает на наличие элемента идентификации. Столбец этого элемента должен отражать метки строк. В противном случае личности нет.

Примечание. Если таблица Кэли симметрична по диагонали, то группа является абелевой.

Циклическая группа -

Это группа, порожденная одним элементом, и этот элемент называется генератором этой циклической группы. или циклическая группа G - это группа, в которой каждый элемент является степенью определенного элемента g в группе. То есть каждый элемент G может быть записан как g ⁿ для некоторого целого числа n для мультипликативной группы или ng для некоторого целого числа n для аддитивной группы. Итак, g - генератор группы G.

Свойства циклической группы:
1. Каждая циклическая группа также является абелевой группой.
2. Если G - циклическая группа с образующей g и порядком n. Если m <n, то порядок элемента g ^m определяется выражением
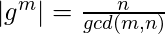
3. Каждая подгруппа циклической группы циклическая.
4. Если G - конечная циклическая группа с порядком n, порядок каждого элемента в G делит n.
5. Если d - положительный делитель числа n, количество элементов порядка d в циклической группе порядка n равно Φ (d), где Φ (d) - функция Эйлера Фи .
6. Порядок циклической группы и порядок ее генератора одинаковый.

Связанные вопросы GATE:
1) Ворота CS 2004
2) Ворота CS 2009

Вниманию читателя! Не переставай учиться сейчас. Ознакомьтесь со всеми важными концепциями теории CS для собеседований по SDE с помощью курса теории CS по доступной для студентов цене и будьте готовы к работе в отрасли.