Связь между собственными векторами и пустым пространством
Предпосылки:
- Собственные векторы
- Nullspace
Некоторые важные моменты о собственных значениях и собственных векторах:
- Собственные значения могут быть комплексными числами даже для вещественных матриц.
- Когда собственные значения становятся сложными, собственные векторы также становятся сложными.
- Если матрица симметрична (например, A = A T ), то собственные значения всегда действительны.
- В результате собственные векторы симметричных матриц также являются действительными.
- Для симметричных матриц всегда будет n линейно независимых собственных векторов.
Теперь давайте обсудим связь между собственными векторами и нулевым пространством.
Из этой статьи мы показываем, что
AX = λX
А теперь позвольте мне задать вам вопрос. Что происходит, когда лямбда равна 0? То есть одно из собственных значений становится 0.
Итак, когда одно из собственных значений становится равным 0, мы получаем это уравнение, которое задается следующим образом:
AX = 0 - (уравнение 1)
Из этой статьи мы показываем, что
AB = 0 - (уравнение 2)
Итак, вы заметили, что формы уравнения 1 и уравнения 2 одинаковы.
Таким образом, это в основном означает, что X, который является собственным вектором, соответствующим собственному значению, лямбда равняется 0 , является вектором нулевого пространства, потому что он имеет именно ту форму, которую мы здесь заметили. Таким образом, можно сказать, что собственные векторы, соответствующие нулевым собственным значениям, находятся в нулевом пространстве исходной матрицы A. И наоборот, если собственное значение, соответствующее собственному вектору, не равно 0 , то этот собственный вектор не может находиться в нулевом пространстве A. Итак, это важные результаты, которые нам необходимо знать.
Итак, вот как собственные векторы связаны с нулевым пространством.
Пример:
Рассмотрим следующую матрицу A
Обратите внимание, что это симметричная матрица, поэтому собственные значения всегда действительны, как я уже говорил ранее в разделе важных моментов.
Собственные значения этой матрицы:
λ = (0, 1, 2)
Собственные векторы, соответствующие этим собственным значениям, равны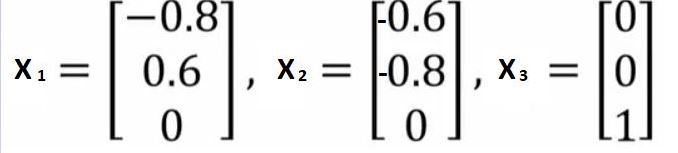
Code: Python code to calculate eigenvalue and eigenvector
# Python program to illustrate# connection between eigenvectors and nullspace # Importing required librariesimport numpy as npfrom numpy import linalg # Taking A matrixA = np.array([ [0.36, 0.48, 0], [0.48, 0.64, 0], [0, 0, 2]]) # Calculating eigenvalues and eigenvectorseigValues, eigVectors = linalg.eig(A) # Printing those valuesprint("Eigenvalue are :", eigValues)print("Eigenvectors are :", eigVectors) # Taking eigenvector 1eigVector1 = np.array([ [-0.8], [0.6], [0]]) # Matrix multiplication between A and eigenvector1result = np.dot(A, eigVector1)# Print the resultprint(result) # This code is contributed by Amiya Rout |
Output: Eigenvalue are : [0. 1. 2.] Eigenvectors are : [[-0.8 -0.6 0. ] [ 0.6 -0.8 0. ] [ 0. 0. 1. ]] [[0.] [0.] [0.]]
Итак, из нашего обсуждения ранее мы заметили, что если X1 является собственным вектором, соответствующим лямбда, равному 0 , то он будет в нулевом пространстве этой матрицы A. Давайте проверим это, умножив A на X1 . Мы проверяем, что
Вы можете легко увидеть, что при выполнении этого вычисления вы получите это (0, 0, 0) , что в основном показывает, что это собственный вектор, соответствующий нулевому собственному значению.
Внимание компьютерщик! Укрепите свои основы с помощью базового курса программирования Python и изучите основы.
Для начала подготовьтесь к собеседованию. Расширьте свои концепции структур данных с помощью курса Python DS. А чтобы начать свое путешествие по машинному обучению, присоединяйтесь к курсу Машинное обучение - базовый уровень.