Свойства z-преобразований

Предварительное условие: что такое Z-преобразование?

Z-преобразование важно для анализа дискретных сигналов и систем. В этой статье мы увидим свойства z-преобразований. Эти свойства полезны при вычислении преобразований сложных дискретных сигналов во временной области.

1. Линейность: если у нас есть две последовательности x ₁ [n] и x ₂ [n] и их индивидуальные z-преобразования как X ₁ (z) и X ₂ (z), то свойство линейности позволяет нам написать:

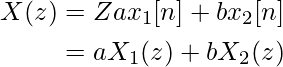
Это легко доказывается. Сначала рассмотрим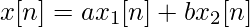

Тогда из определения мы видим:

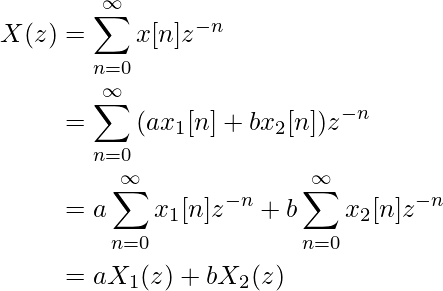
2. Сдвиг во времени. Если у нас есть последовательность со сдвигом во времени, такая как x[nk], то ее z-преобразование задается как Z{x[nk]} = z^{-k}X(z).

Возьмем n – k = m, т. е. n = k + m и y[n] = x[nk]. Здесь мы предполагаем, что x[n] начинается с n=0, следовательно, x[nk] начинается с n=k, или nk=0, или с m=0.

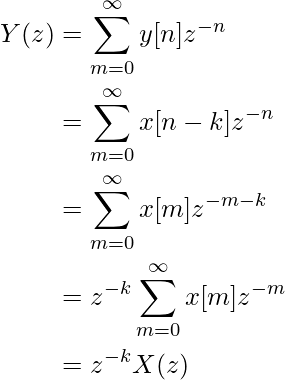
3. Обращение времени: свойство обращения времени гласит, что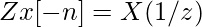

Мы собираемся формально доказать это утверждение, взяв y[n]=x[-n].

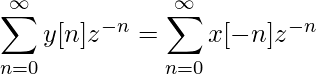
Теперь возьмем -n=m. затем

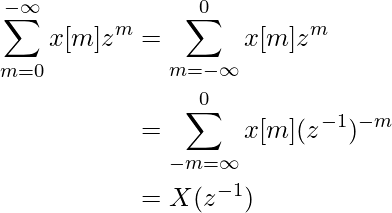
4. Масштабирование в области z: когда мы умножаем последовательность сигналов x[ ⁿ ] во временной области на экспоненциальный коэффициент an, эквивалентное z-преобразование нового сигнала масштабируется с коэффициентом a.

В принципе, .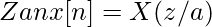

Доказательство элементарно и показано ниже.

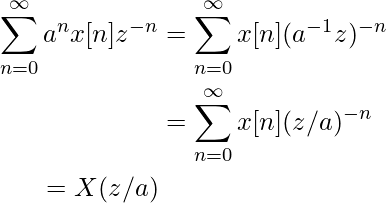
5. Дифференциация в области z: Мы знаем: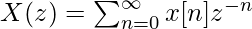

Дифференцируя по z, получаем

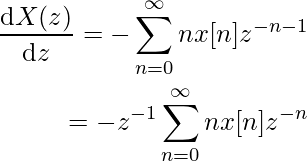
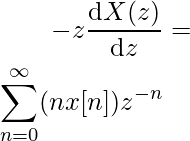
Отсюда мы можем сделать вывод, что для k дифференцирований мы получаем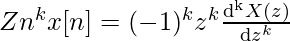

6. Свертка. Свертка двух последовательностей x[n] и h[n] определяется как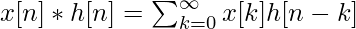

Теперь z-преобразования x[n] и h[n] — это X(z) и H(z) соответственно. Используя это обозначение, мы имеем

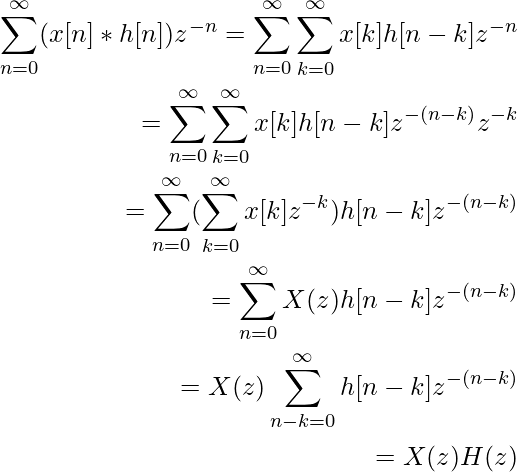
Следовательно, свертка во временной области — это умножение в области z.

7. Теорема о начальном значении. Теорема о начальном значении дает нам инструмент для вычисления начального значения последовательности x[n], то есть x[0] в области z, путем ограничения значения X(z). Он утверждает, что возможна следующая эквивалентность.

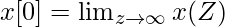
Доказательство, как и прежде, опирается на определение X(z).

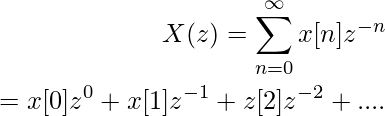
Ясно, что если мы хотим получить x[0], мы можем приблизить z к бесконечности так, чтобы все остальные члены исчезли. То, что осталось позади, — это именно формулировка ранее представленной теоремы.

8. Теорема об окончательном значении. Теорема об окончательном значении позволяет нам узнать окончательное значение x[n] или значение x[n на бесконечности], используя соответствующие пределы X(z).

В нем говорится, что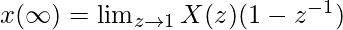

Если мы возьмем z-преобразование x[n]-x[n-1], то получим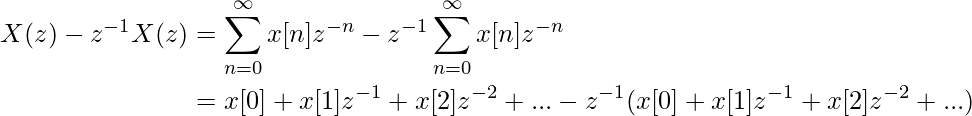

Переходя теперь к пределу z⇢1, мы видим, что получаем 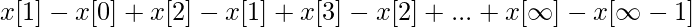в правой части, что в основном упрощается до x[infty]. Следовательно, теорема доказана.