Создайте DFA, чтобы принять двоичную строку, содержащую «01» i раз и «1» 2j раз.

Опубликовано: 9 Января, 2022

Учитывая двоичную строку str , задача состоит в том, чтобы построить DFA, который принимает данную двоичную строку, если она содержит «01» i раз и «1» 2j раз, т. Е.

Примеры:

Input: str = “011111”
Output: Accepted
Explanation:
The string follows the language as: (01)¹(1)^2*2
Input: str = “01111”
Output: Not Accepted

Рекомендуется: сначала попробуйте свой подход в {IDE}, прежде чем переходить к решению.

DFA или детерминированные конечные автоматы - это конечный автомат, который принимает строку (при определенных условиях), если она достигает конечного состояния, в противном случае отклоняет ее.
В DFA нет понятия памяти, поэтому мы должны проверять строку посимвольно, начиная с 0-го символа. Вводимый набор символов для задачи: {0, 1}. Чтобы DFA был действительным, должно быть определено правило перехода для каждого символа входного набора в каждом состоянии в допустимое состояние. Поэтому для разработки DFA выполняются следующие шаги:

Создайте начальную стадию и переведите 0 и 1 в следующее возможное состояние.
За переходом 0 всегда следует переход 1.
Сделайте начальное состояние и переведите его входные алфавиты, то есть 0 и 1, в два разных состояния.
Проверяйте соответствие строки после каждого перехода, чтобы игнорировать ошибки.
Сначала сделайте DfA для строки минимальной длины, затем продолжайте шаг за шагом.
Определите конечное состояние (я) в соответствии с приемлемостью строки.

Пошаговый подход к разработке DFA:

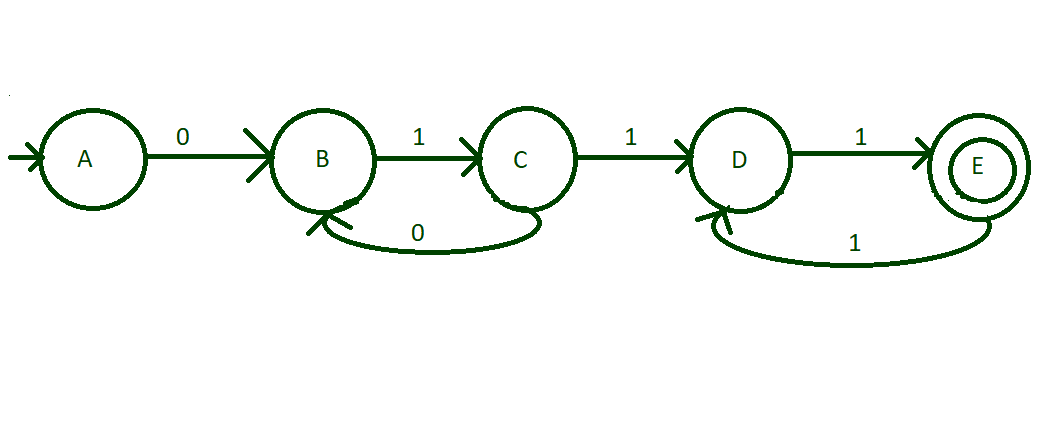
Шаг 1: Минимально возможная допустимая строка - 0111, т. Е. (01) ¹ (11) ¹ . Итак, создайте начальное состояние «A», в котором выполняется переход 0 в состояние «B», а затем переход 1 из «B» в состояние «C», затем переход 1 из «C» в «D», затем переход 1 от «D» до «E», как показано на диаграмме, делают этот этап «E» конечным состоянием.

Шаг 2: Теперь представьте, что строка имеет последовательный (01), за которым следует последовательный (11), чтобы закончить строку. Следовательно, когда i> 1, выполните переход «0» из состояния «C» в состояние «B» и выполните переход «1» из состояния «E» в состояние «D». Следовательно, теперь допустимы строки типа 010111, 011111, 0101111111 и т. Д.

Шаг 3: Мы закончили со всеми возможными строками. Но есть несколько входных алфавитов, которые не переходят ни в одно из состояний. В этом случае все эти входные данные будут отправлены в какое-то мертвое состояние, чтобы заблокировать их дальнейшие переходы, которые недопустимы. Входные алфавиты мертвого состояния будут отправлены в само мертвое состояние. Таким образом, окончательный дизайн DFA:

Below is the implementation of the above approach:

Java

// Java code for the above DFA
import java.util.*;
 
class GFG{
   
// Function for the state A
static void checkstatea(String n)
{
  if (n.length() % 2 != 0 ||
      n.length() < 4)
    System.out.print("string not accepted");
  else
  {   
    int i = 0;
     
    // State transition to B
    // if the character is 0
    if (n.charAt(i) == "0")
      stateb(n.substring(1));
    else
      System.out.print("string not accepted");
  }
}
  
// Function for the state B
static void stateb(String n)
{
  int i = 0;
   
  if (n.charAt(i) == "0")
    System.out.print("string not accepted");
  
  // State transition to C
  // if the character is 1
  else
    statec(n.substring(1));
}
   
// Function for the state C
static void statec(String n)
{
  int i = 0;
   
  // State transition to D
  // if the character is 1
  if (n.charAt(i) == "1")
    stated(n.substring(1));
  
  // State transition to B
  // if the character is 0
  else
    stateb(n.substring(1));
}
  
// Function for the state D
static void stated(String n)
{
  int i = 0;
   
  if (n.length() == 1)
  {
    if (n.charAt(i) == "1")
      System.out.print("string accepted");
    else
      System.out.print("string not accepted");
  }
  else
  {
     
    // State transition to E
    // if the character is 1
    if (n.charAt(i) == "1")
      statee(n.substring(1));
    else
      System.out.print("string not accepted");
  }
}
  
// Function for the state E    
static void statee(String n)
{
  int i = 0;
   
  if (n.length() == 1)
  {
    if (n.charAt(i) == "0")
      System.out.print("string not accepted");
    else
      System.out.print("string accepted");
  }
  else
  {
    if (n.charAt(i) == "0")
      System.out.print("string not accepted");
     
    stated(n.substring(1));
  }
}
      
// Driver code
public static void main(String []args)
{
   
  // Take string input
  String n ="011111";
  
  // Call stateA to check the input
  checkstatea(n);
}
}
 
// This code is contributed by pratham76

Python3

# Python3 program for the given
# language
 
# Function for the state A
def checkstatea(n):
    if(len(n)%2!=0 or len(n)<4):
        print("string not accepted")
    else:   
        i=0
 
        # State transition to B
        # if the character is 0
        if(n[i]=="0"):
            stateb(n[1:])
        else:
            print("string not accepted")
 
# Function for the state B
def stateb(n):
    i=0
    if(n[i]=="0"):
        print("string not accepted")
 
    # State transition to C
    # if the character is 1
    else:
        statec(n[1:])
 
# Function for the state C
def statec(n):
    i=0
 
    # State transition to D
    # if the character is 1
    if(n[i]=="1"):
        stated(n[1:])
 
    # State transition to B
    # if the character is 0
    else:
        stateb(n[1:])
 
# Function for the state D
def stated(n):
    i=0
    if(len(n)==1):
        if(n[i]=="1"):
            print("string accepted")
        else:
            print("string not accepted")
    else:
 
        # State transition to E
        # if the character is 1
        if(n[i]=="1"):
            statee(n[1:])
        else:
            print("string not accepted")  
 
# Function for the state E    
def statee(n):
    i=0
    if(len(n)==1):
        if(n[i]=="0"):
            print("string not accepted")
        else:
            print("string accepted")
          
    else:
        if(n[i]=="0"):
            print("string not accepted")
        stated(n[1:])
      
      
# Driver code
if __name__ == "__main__":
 
    n = "011111"
    checkstatea(n)
    

C#

// C# code for the above DFA
using System;
using System.Collections;
using System.Collections.Generic;
class GFG{
     
// Function for the state A
static void checkstatea(string n)
{
  if(n.Length % 2 != 0 ||
     n.Length < 4)
    Console.Write("string not accepted");
  else
  {   
    int i = 0;
 
    // State transition to B
    // if the character is 0
    if(n[i] == "0")
      stateb(n.Substring(1));
    else
      Console.Write("string not accepted");
  }
}
 
// Function for the state B
static void stateb(string n)
{
  int i = 0;
  if(n[i] == "0")
    Console.Write("string not accepted");
 
  // State transition to C
  // if the character is 1
  else
    statec(n.Substring(1));
}
  
// Function for the state C
static void statec(string n)
{
  int i = 0;
 
  // State transition to D
  // if the character is 1
  if(n[i] == "1")
    stated(n.Substring(1));
 
  // State transition to B
  // if the character is 0
  else
    stateb(n.Substring(1));
}
 
// Function for the state D
static void stated(string n)
{
  int i = 0;
  if(n.Length == 1)
  {
    if(n[i] == "1")
      Console.Write("string accepted");
    else
      Console.Write("string not accepted");
  }
  else
  {
    // State transition to E
    // if the character is 1
    if(n[i] == "1")
      statee(n.Substring(1));
    else
      Console.Write("string not accepted");
  }
}
 
// Function for the state E    
static void statee(string n)
{
  int i = 0;
  if(n.Length == 1)
  {
    if(n[i] == "0")
      Console.Write("string not accepted");
    else
      Console.Write("string accepted");
  }
  else
  {
    if(n[i] == "0")
      Console.Write("string not accepted");
    stated(n.Substring(1));
  }
}
     
// Driver code
public static void Main(string []args)
{
  // Take string input
  string n ="011111";
 
  // Call stateA to check the input
  checkstatea(n);
}
}
 
// This code is contributed by rutvik_56

Output:

string accepted

Вниманию читателя! Не прекращайте учиться сейчас. Освойте все важные концепции DSA с помощью самостоятельного курса DSA по приемлемой для студентов цене и будьте готовы к работе в отрасли. Чтобы завершить подготовку от изучения языка к DS Algo и многому другому, см. Полный курс подготовки к собеседованию .

Если вы хотите посещать живые занятия с отраслевыми экспертами, пожалуйста, обращайтесь к Geeks Classes Live и Geeks Classes Live USA.

Алгоритмы

Создайте DFA, чтобы принять двоичную строку, содержащую «01» i раз и «1» 2j раз.

Java

Python3

C#

РЕКОМЕНДУЕМЫЕ СТАТЬИ