Сложность различных операций в двоичном дереве, двоичном дереве поиска и дереве AVL
В этой статье мы обсудим сложность различных операций в двоичных деревьях, включая деревья BST и AVL. Прежде чем понимать эту статью, вы должны иметь общее представление о двоичном дереве, двоичном дереве поиска и дереве AVL.
Основные операции в двоичном дереве: поиск, вставка и удаление. Мы увидим наихудший случай временной сложности этих операций в двоичных деревьях.
Двоичное дерево -
В двоичном дереве узел может иметь не более двух дочерних элементов. Рассмотрим скошенное влево двоичное дерево, показанное на рисунке 1.
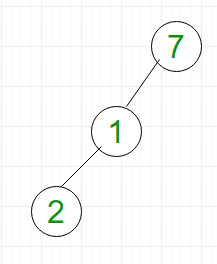
- Поиск: для поиска элемента 2 мы должны пройти по всем элементам (при условии, что мы выполняем обход в ширину). Следовательно, поиск в двоичном дереве имеет сложность наихудшего случая O (n).
- Вставка: чтобы вставить элемент как левый дочерний элемент 2, мы должны пройти все элементы. Следовательно, вставка в двоичное дерево имеет сложность наихудшего случая O (n).
- Удаление: для удаления элемента 2 мы должны пройти по всем элементам, чтобы найти 2 (при условии, что мы выполняем обход в ширину). Следовательно, удаление в двоичном дереве имеет сложность наихудшего случая O (n).
Дерево двоичного поиска (BST) -
BST - это особый тип двоичного дерева, в котором левый дочерний элемент узла имеет значение меньше, чем родительский, а правый дочерний элемент имеет значение больше, чем родительский. Рассмотрим скошенный влево BST, показанный на рисунке 2.
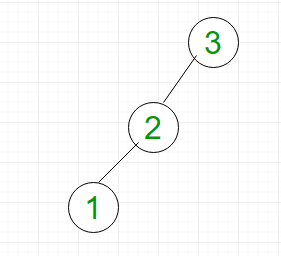
- Поиск: для поиска элемента 1 мы должны пройти по всем элементам (в порядке 3, 2, 1). Следовательно, поиск в двоичном дереве поиска имеет сложность наихудшего случая O (n). В общем, временная сложность равна O (h), где h - высота BST.
- Вставка: для вставки элемента 0 он должен быть вставлен как левый дочерний элемент 1. Следовательно, нам нужно пройти все элементы (в порядке 3, 2, 1), чтобы вставить 0, который имеет сложность наихудшего случая O (n). В общем, временная сложность O (h).
- Удаление: для удаления элемента 1 мы должны пройти по всем элементам, чтобы найти 1 (в порядке 3, 2, 1). Следовательно, удаление в двоичном дереве имеет сложность наихудшего случая O (n). В общем, временная сложность O (h).
AVL / Дерево со сбалансированной высотой -
Дерево AVL - это двоичное дерево поиска с дополнительным свойством, заключающееся в том, что разница между высотой левого поддерева и правого поддерева любого узла не может быть больше 1. Например, BST, показанный на рисунке 2, не является AVL, поскольку разница между левым поддеревом. -дерево и правое поддерево узла 3 равно 2. Однако BST, показанный на рисунке 3, является деревом AVL.
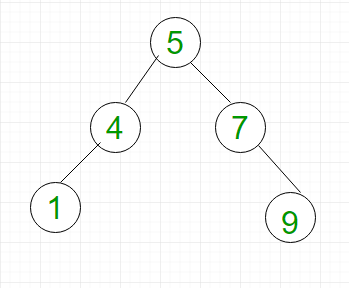
- Поиск: для поиска элемента 1 мы должны пройти элементы (в порядке 5, 4, 1) = 3 = log 2 n. Следовательно, поиск в дереве AVL имеет сложность наихудшего случая O (log 2 n).
- Вставка: для вставки элемента 12 он должен быть вставлен как правый дочерний элемент 9. Следовательно, нам нужно пройти элементы (в порядке 5, 7, 9), чтобы вставить 12, сложность наихудшего случая равна O (log 2 n).
- Удаление: для удаления элемента 9 мы должны пройти по элементам, чтобы найти 9 (в порядке 5, 7, 9). Следовательно, удаление в двоичном дереве имеет сложность наихудшего случая O (log 2 n).
Мы обсудим вопросы, основанные на сложности операций с бинарными деревьями.
Que-1. Какова наихудшая временная сложность операций поиска, вставки и удаления в общем дереве двоичного поиска?
(A) O (n) для всех
(B) O (Logn) для всех
(C) O (Logn) для поиска и вставки и O (n) для удаления
(D) O (Logn) для поиска и O (n) для вставки и удаления
Решение: Как обсуждалось, все операции в BST имеют временную сложность наихудшего случая O (n). Итак, правильный вариант - (А).
Que-2. Каковы наихудшие временные сложности поиска в двоичном дереве, дереве BST и AVL соответственно?
(A) O (n) для всех
(B) O (Logn) для всех
(C) O (n) для двоичного дерева и O (Logn) для других
(D) O (n) для двоичного дерева и BST и O (Logn) для AVL
Решение: Как обсуждалось, операция поиска в двоичном дереве и BST имеет временную сложность наихудшего случая O (n). Однако дерево AVL имеет наихудшую временную сложность O (logn). Итак, правильный вариант - (D).