Самый большой треугольник Рёло в квадрате, вписанном в прямоугольный треугольник
Дан прямоугольный треугольник с высотой l , основанием b и гипотенузой h , вписывающий квадрат, который, в свою очередь, вписывает треугольник Рило. Задача состоит в том, чтобы найти максимально возможную площадь этого треугольника Рило.
Примеры:
Ввод: l = 5, b = 12, h = 13. Выход: 8.77914 Ввод: l = 3, b = 4, h = 5. Выход: 2,07116
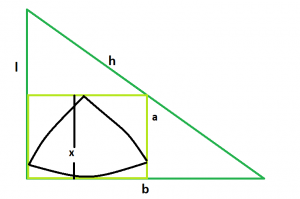
Подход : мы знаем, что сторона квадрата, вписанного в прямоугольный треугольник, равна a = (l * b) / (l + b) , см. Площадь наибольшего квадрата, вписанного в прямоугольный треугольник.
Кроме того, в треугольнике Рело x = a .
Итак, x = (l * b) / (l + b) .
Итак, площадь треугольника Рело равна, A = 0,70477 * x ^ 2 = 0,70477 * ((l * b) / (l + b)) ^ 2 .
Ниже представлена реализация описанного выше подхода:
Вниманию читателя! Не прекращайте учиться сейчас. Освойте все важные концепции DSA с помощью самостоятельного курса DSA по приемлемой для студентов цене и будьте готовы к работе в отрасли. Чтобы завершить подготовку от изучения языка к DS Algo и многому другому, см. Полный курс подготовки к собеседованию .
Если вы хотите посещать живые занятия с отраслевыми экспертами, пожалуйста, обращайтесь к Geeks Classes Live и Geeks Classes Live USA.