Расстояние между двумя параллельными плоскостями в 3-D

Опубликовано: 16 Января, 2022

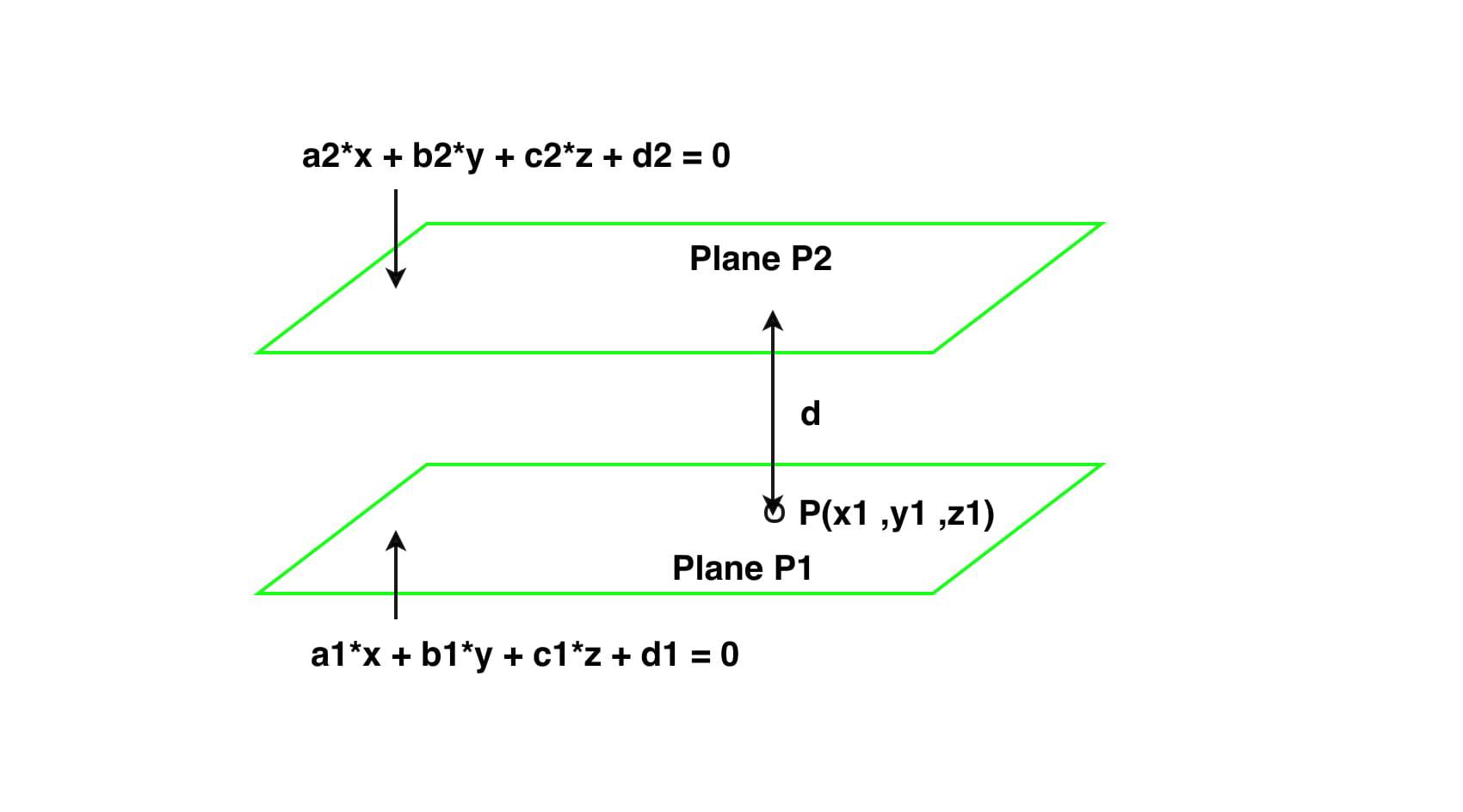
Вам даны две плоскости P1 : a1 * x + b1 * y + c1 * z + d1 = 0 и P2 : a2 * x + b2 * y + c2 * z + d2 = 0 . Задача - написать программу для определения расстояния между этими двумя плоскостями.

Примеры :

 Ввод: a1 = 1, b1 = 2, c1 = -1, d1 = 1, a2 = 3, b2 = 6, c2 = -3, d2 = -4
Выход: расстояние 0,952579344416

Ввод: a1 = 1, b1 = 2, c1 = -1, d1 = 1, a2 = 1, b2 = 6, c2 = -3, d2 = -4
Вывод: плоскости не параллельны

Рекомендуется: сначала попробуйте свой подход в {IDE}, прежде чем переходить к решению.

Подход: Рассмотрим две плоскости, заданные уравнениями: -

P1 : a1 * x + b1 * y + c1 * z + d1 = 0, where a1, b1 and c1, d1 are real constants and 
P2 : a2 * x + b2 * y + c2 * z + d2 = 0, where a2, b2 and c2, d2 are real constants.

Условие параллельности двух плоскостей:

 => a1 / a2 = b1 / b2 = c1 / c2

Найдите точку в любой одной плоскости, расстояние от которой до другой плоскости будет расстоянием между этими двумя плоскостями. Расстояние можно рассчитать по формулам:

 Расстояние = (| a * x1 + b * y1 + c * z1 + d |) / (sqrt (a * a + b * b + c * c))

Пусть точка в плоскости P1 есть P (x1, y1, z1),
Положите x = y = 0 в уравнение a1 * x + b1 * y + c1 * z + d1 = 0 и найдите z.
=> z = -d1 / c1
Теперь у нас есть координаты P (0, 0, z) = P (x1, y1, z1).
Расстояние от точки P до плоскости P2 будет: -

Distance = (| a2*x1 + b2*y1 + c2*z1 + d2 |) / (sqrt( a2*a2 + b2*b2 + c2*c2)) 
= (| a2*0 + b2*0 + c2*z1 + d2 |) / (sqrt( a2*a2 + b2*b2 + c2*c2)) 
= (| c2*z1 + d2 |) / (sqrt( a2*a2 + b2*b2 + c2*c2)) 
 

Below is the implementation of the above formulae: 
 

C++

// C++ program to find the Distance
// between two parallel Planes in 3 D.
#include <bits/stdc++.h>
#include<math.h>
 
using namespace std;
 
// Function to find distance
void distance(float a1, float b1,
              float c1, float d1,
              float a2, float b2,
              float c2, float d2)
{
    float x1, y1, z1, d;
    if (a1 / a2 == b1 / b2 &&
        b1 / b2 == c1 / c2)
    {
        x1 = y1 = 0;
        z1 = -d1 / c1;
        d = fabs(( c2 * z1 + d2)) /
           (sqrt(a2 * a2 + b2 *
                 b2 + c2 * c2));
        cout << "Perpendicular distance is "
             << d << endl;
    }
    else
        cout << "Planes are not parallel";
    return;
}
 
// Driver Code
int main()
{
    float a1 = 1;
    float b1 = 2;
    float c1 = -1;
    float d1 = 1;
    float a2 = 3;
    float b2 = 6;
    float c2 = -3;
    float d2 = -4;
    distance(a1, b1, c1, d1,
             a2, b2, c2, d2); // Fxn cal
    return 0;
}
 
// This code is contributed
// by Akanksha Rai(Abby_akku)

C

// C program to find the Distance between
// two parallel Planes in 3 D.
  
#include <stdio.h>
#include<math.h>
  
// Function to find distance
void distance(float a1, float b1, float c1,
            float d1, float a2, float b2,
            float c2, float d2)
{
    float x1,y1,z1,d;
    if (a1 / a2 == b1 / b2 && b1 / b2 == c1 / c2)
    {
        x1 = y1 = 0;
        z1 =-d1 / c1;
        d = fabs(( c2 * z1 + d2)) / (sqrt(a2 * a2 + b2 * b2 + c2 * c2));
        printf("Perpendicular distance is %f ", d);
    }
    else
        printf("Planes are not parallel");
    return;
}
   
// Driver Code
int main()
{
    float a1 = 1;
    float b1 = 2;
    float c1 = -1;
    float d1 = 1;
    float a2 = 3;
    float b2 = 6;
    float c2 = -3;
    float d2 = -4;
    distance(a1, b1, c1, d1, a2, b2, c2, d2);     // Fxn cal
    return 0;
}
   
// This code is contributed 
// by Amber_Saxena.

Java

// Java program to find the Distance
// between two parallel Planes in 3 D.
import java .io.*;
import java.lang.Math;
 
class GFG
{
     
// Function to find distance
static void distance(float a1, float b1, float c1,
                     float d1, float a2, float b2,
                     float c2, float d2)
{
     
    float x1,y1,z1,d;
    if (a1 / a2 == b1 / b2 &&
        b1 / b2 == c1 / c2)
    {
        x1 = y1 = 0;
        z1 =-d1 / c1;
        d = Math.abs(( c2 * z1 + d2)) /
            (float)(Math.sqrt(a2 * a2 + b2 *
                              b2 + c2 * c2));
        System.out.println("Perpendicular distance is "+ d);
    }
    else
        System.out.println("Planes are not parallel");
}
 
// Driver code
public static void main(String[] args)
{
    float a1 = 1;
    float b1 = 2;
    float c1 = -1;
    float d1 = 1;
    float a2 = 3;
    float b2 = 6;
    float c2 = -3;
    float d2 = -4;
    distance(a1, b1, c1, d1,
             a2, b2, c2, d2);// Fxn cal
}
}
 
// This code is contributed
// by Amber_Saxena.

Python

# Python program to find the Distance between
# two parallel Planes in 3 D.
 
import math
 
# Function to find distance
def distance(a1, b1, c1, d1, a2, b2, c2, d2):
     
    if (a1 / a2 == b1 / b2 and b1 / b2 == c1 / c2):
        x1 = y1 = 0
        z1 =-d1 / c1
        d = abs(( c2 * z1 + d2)) / (math.sqrt(a2 * a2 + b2 * b2 + c2 * c2))
        print("Perpendicular distance is"), d
    else:
        print("Planes are not parallel")
 
# Driver Code
a1 = 1
b1 = 2
c1 = -1
d1 = 1
a2 = 3
b2 = 6
c2 = -3
d2 = -4
distance(a1, b1, c1, d1, a2, b2, c2, d2)     # Fxn cal

C#

// C# program to find the Distance
// between two parallel Planes in 3 D.
using System;
 
class GFG
{
     
// Function to find distance
static void distance(float a1, float b1,
                     float c1, float d1,
                     float a2, float b2,
                     float c2, float d2)
{
    float z1, d;
    if (a1 / a2 == b1 / b2 &&
        b1 / b2 == c1 / c2)
    {
         
        z1 =-d1 / c1;
        d = Math.Abs((c2 * z1 + d2)) /
            (float)(Math.Sqrt(a2 * a2 + b2 *
                              b2 + c2 * c2));
        Console.Write("Perpendicular distance is " + d);
    }
    else
        Console.Write("Planes are not parallel");
}
 
// Driver code
public static void Main()
{
    float a1 = 1;
    float b1 = 2;
    float c1 = -1;
    float d1 = 1;
    float a2 = 3;
    float b2 = 6;
    float c2 = -3;
    float d2 = -4;
    distance(a1, b1, c1, d1,
             a2, b2, c2, d2);// Fxn cal
}
}
 
// This code is contributed
// by ChitraNayal

PHP

<?php
// PHP program to find the Distance
// between two parallel Planes in 3 D
 
// Function to find distance
function distance($a1, $b1, $c1,
                  $d1, $a2, $b2,
                  $c2, $d2)
{
    if ($a1 / $a2 == $b1 / $b2 &&
        $b1 / $b2 == $c1 / $c2)
    {
        $x1 = $y1 = 0;
        $z1 =- $d1 / $c1;
        $d = abs(($c2 * $z1 + $d2)) /
            (sqrt($a2 * $a2 + $b2 *
                  $b2 + $c2 * $c2));
        echo "Perpendicular distance is ", $d;
    }
    else
        echo "Planes are not parallel";
}
 
// Driver Code
$a1 = 1;
$b1 = 2;
$c1 = -1;
$d1 = 1;
$a2 = 3;
$b2 = 6;
$c2 = -3;
$d2 = -4;
distance($a1, $b1, $c1, $d1,
         $a2, $b2, $c2, $d2);    
 
// This code is contributed
// by Amber_Saxena.
?>

Javascript

<script>
 
// Javascript program to find the Distance
// between two parallel Planes in 3 D.
 
// Function to find distance
function distance(a1, b1, c1,
                     d1,  a2, b2,
                     c2, d2)
{
     
    let x1,y1,z1,d;
    if (a1 / a2 == b1 / b2 &&
        b1 / b2 == c1 / c2)
    {
        x1 = y1 = 0;
        z1 =-d1 / c1;
        d = Math.abs(( c2 * z1 + d2)) /
            (Math.sqrt(a2 * a2 + b2 *
                              b2 + c2 * c2));
        document.write("Perpendicular distance is "+ d);
    }
    else
        document.write("Planes are not parallel");
}
 
// Driver Code
 
     let a1 = 1;
    let b1 = 2;
    let c1 = -1;
    let d1 = 1;
    let a2 = 3;
    let b2 = 6;
    let c2 = -3;
    let d2 = -4;
    distance(a1, b1, c1, d1,
             a2, b2, c2, d2);// Fxn cal
            
</script>
Output: 
Perpendicular distance is 0.952579344416

 

Вниманию читателя! Не прекращайте учиться сейчас. Освойте все важные концепции DSA с помощью самостоятельного курса DSA по приемлемой для студентов цене и будьте готовы к работе в отрасли. Чтобы завершить подготовку от изучения языка к DS Algo и многому другому, см. Полный курс подготовки к собеседованию .

Если вы хотите посещать живые занятия с отраслевыми экспертами, пожалуйста, обращайтесь к Geeks Classes Live и Geeks Classes Live USA.

РЕКОМЕНДУЕМЫЕ СТАТЬИ