QuickSort

Опубликовано: 21 Января, 2022

Как и сортировка слиянием, QuickSort - это алгоритм «разделяй и властвуй». Он выбирает элемент как опорный элемент и разбивает данный массив вокруг выбранной опорной точки. Существует множество различных версий quickSort, которые выбирают точку поворота по-разному.

Всегда выбирайте первый элемент в качестве опорного.
Всегда выбирайте последний элемент как опорный (реализовано ниже)
Выберите случайный элемент в качестве стержня.
Выберите медианное значение в качестве точки поворота.

Ключевым процессом в quickSort является partition (). Целью разделов является, учитывая массив и элемент x массива в качестве точки поворота, поместите x в его правильную позицию в отсортированном массиве и поместите все меньшие элементы (меньше x) перед x и поместите все большие элементы (больше x) после Икс. Все это нужно делать за линейное время.

Псевдокод для рекурсивной функции QuickSort:

 / * низкий -> начальный индекс, высокий -> конечный индекс * /
quickSort (прибл [], низкий, высокий)
{
    если (низкий <высокий)
    {
        / * pi - индекс разделения, теперь arr [pi]
           в нужном месте * /
        pi = раздел (arr, low, high);

        quickSort (arr, low, pi - 1); // Перед пи
        quickSort (arr, pi + 1, high); // После числа пи
    }
}

Алгоритм разбиения
Может быть много способов выполнить разделение, следующий псевдокод принимает метод, указанный в книге CLRS. Логика проста, мы начинаем с самого левого элемента и отслеживаем индекс меньших (или равных) элементов как i. Если при обходе мы находим меньший элемент, мы меняем местами текущий элемент на arr [i]. В противном случае мы игнорируем текущий элемент.

/* low  --> Starting index,  high  --> Ending index */
quickSort(arr[], low, high)
{
    if (low < high)
    {
        /* pi is partitioning index, arr[pi] is now
           at right place */
        pi = partition(arr, low, high);

        quickSort(arr, low, pi - 1);  // Before pi
        quickSort(arr, pi + 1, high); // After pi
    }
}

Псевдокод для раздела ()

 / * Эта функция принимает последний элемент как опорный, размещает
   элемент поворота в правильном положении в отсортированном
    массив, и помещает все меньшие (меньшие, чем точка поворота)
   слева от оси и все более крупные элементы справа
   оси * /
раздел (обр [], низкий, высокий)
{
    // поворот (элемент будет помещен в правильное положение)
    pivot = arr [высокий];  
 
    i = (low - 1) // Индекс меньшего элемента и указывает 
                   // найдена правильная позиция точки поворота

    для (j = низкий; j <= высокий - 1; j ++)
    {
        // Если текущий элемент меньше, чем точка поворота
        если (arr [j] <точка поворота)
        {
            i ++; // увеличиваем индекс меньшего элемента
            поменять местами arr [i] и arr [j]
        }
    }
    поменять местами arr [i + 1] и arr [high])
    возврат (я + 1)
}

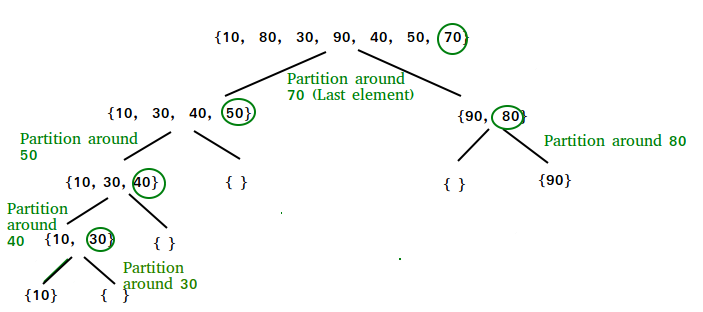
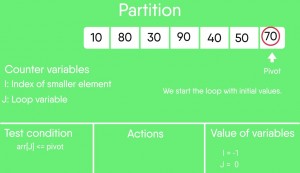
Иллюстрация раздела ():

 arr [] = {10, 80, 30, 90, 40, 50, 70}
Индексы: 0 1 2 3 4 5 6 

low = 0, high = 6, pivot = arr [h] = 70
Инициализировать индекс меньшего элемента, i = -1

Элементы траверсы от j = low to high-1
j = 0 : Поскольку arr [j] <= pivot, выполните i ++ и поменяйте местами (arr [i], arr [j])
я = 0
arr [] = {10, 80, 30, 90, 40, 50, 70} // Без изменений как i и j 
                                     // такие же

j = 1 : Поскольку arr [j]> pivot, ничего не делать
// Без изменений в i и arr []

j = 2 : Поскольку arr [j] <= pivot, выполните i ++ и поменяйте местами (arr [i], arr [j])
я = 1
arr [] = {10, 30, 80, 90, 40, 50, 70} // Мы меняем местами 80 и 30 

j = 3 : Поскольку arr [j]> pivot, ничего не делать
// Без изменений в i и arr []

j = 4 : Поскольку arr [j] <= pivot, выполните i ++ и поменяйте местами (arr [i], arr [j])
я = 2
arr [] = {10, 30, 40, 90, 80, 50, 70} // 80 и 40 поменяны местами
j = 5 : Поскольку arr [j] <= pivot, выполните i ++ и замените arr [i] на arr [j] 
я = 3
arr [] = {10, 30, 40, 50, 80, 90, 70} // 90 и 50 поменяны местами 

Мы выходим из цикла, потому что j теперь равно high-1.
Наконец, мы устанавливаем ось в правильное положение, меняя местами
arr [i + 1] и arr [high] (или поворот) 
arr [] = {10, 30, 40, 50, 70, 90, 80} // 80 и 70 поменяны местами 

Теперь 70 на своем месте. Все элементы меньше, чем
70 перед ним, а все элементы больше 70 - после
Это.

Рекомендуется: сначала решите эту проблему на «ПРАКТИКЕ», прежде чем переходить к решению.

Implementation:
Following are the implementations of QuickSort:

C++14

/* C++ implementation of QuickSort */
#include <bits/stdc++.h>
using namespace std;
 
// A utility function to swap two elements
void swap(int* a, int* b)
{
    int t = *a;
    *a = *b;
    *b = t;
}
 
/* This function takes last element as pivot, places
the pivot element at its correct position in sorted
array, and places all smaller (smaller than pivot)
to left of pivot and all greater elements to right
of pivot */
int partition (int arr[], int low, int high)
{
    int pivot = arr[high]; // pivot
    int i = (low - 1); // Index of smaller element and indicates the right position of pivot found so far
 
    for (int j = low; j <= high - 1; j++)
    {
        // If current element is smaller than the pivot
        if (arr[j] < pivot)
        {
            i++; // increment index of smaller element
            swap(&arr[i], &arr[j]);
        }
    }
    swap(&arr[i + 1], &arr[high]);
    return (i + 1);
}
 
/* The main function that implements QuickSort
arr[] --> Array to be sorted,
low --> Starting index,
high --> Ending index */
void quickSort(int arr[], int low, int high)
{
    if (low < high)
    {
        /* pi is partitioning index, arr[p] is now
        at right place */
        int pi = partition(arr, low, high);
 
        // Separately sort elements before
        // partition and after partition
        quickSort(arr, low, pi - 1);
        quickSort(arr, pi + 1, high);
    }
}
 
/* Function to print an array */
void printArray(int arr[], int size)
{
    int i;
    for (i = 0; i < size; i++)
        cout << arr[i] << " ";
    cout << endl;
}
 
// Driver Code
int main()
{
    int arr[] = {10, 7, 8, 9, 1, 5};
    int n = sizeof(arr) / sizeof(arr[0]);
    quickSort(arr, 0, n - 1);
    cout << "Sorted array: 
";
    printArray(arr, n);
    return 0;
}
 
// This code is contributed by rathbhupendra

Java

// Java implementation of QuickSort
import java.io.*;
 
class GFG{
     
// A utility function to swap two elements
static void swap(int[] arr, int i, int j)
{
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}
 
/* This function takes last element as pivot, places
   the pivot element at its correct position in sorted
   array, and places all smaller (smaller than pivot)
   to left of pivot and all greater elements to right
   of pivot */
static int partition(int[] arr, int low, int high)
{
     
    // pivot
    int pivot = arr[high];
     
    // Index of smaller element and
    // indicates the right position
    // of pivot found so far
    int i = (low - 1);
 
    for(int j = low; j <= high - 1; j++)
    {
         
        // If current element is smaller
        // than the pivot
        if (arr[j] < pivot)
        {
             
            // Increment index of
            // smaller element
            i++;
            swap(arr, i, j);
        }
    }
    swap(arr, i + 1, high);
    return (i + 1);
}
 
/* The main function that implements QuickSort
          arr[] --> Array to be sorted,
          low --> Starting index,
          high --> Ending index
 */
static void quickSort(int[] arr, int low, int high)
{
    if (low < high)
    {
         
        // pi is partitioning index, arr[p]
        // is now at right place
        int pi = partition(arr, low, high);
 
        // Separately sort elements before
        // partition and after partition
        quickSort(arr, low, pi - 1);
        quickSort(arr, pi + 1, high);
    }
}
 
// Function to print an array
static void printArray(int[] arr, int size)
{
    for(int i = 0; i < size; i++)
        System.out.print(arr[i] + " ");
         
    System.out.println();
}
 
// Driver Code
public static void main(String[] args)
{
    int[] arr = { 10, 7, 8, 9, 1, 5 };
    int n = arr.length;
     
    quickSort(arr, 0, n - 1);
    System.out.println("Sorted array: ");
    printArray(arr, n);
}
}
 
// This code is contributed by Ayush Choudhary

Python3

# Python3 implementation of QuickSort 
 
# This Function handles sorting part of quick sort
# start and end points to first and last element of
# an array respectively
def partition(start, end, array):
     
    # Initializing pivot"s index to start
    pivot_index = start
    pivot = array[pivot_index]
     
    # This loop runs till start pointer crosses
    # end pointer, and when it does we swap the
    # pivot with element on end pointer
    while start < end:
         
        # Increment the start pointer till it finds an
        # element greater than  pivot
        while start < len(array) and array[start] <= pivot:
            start += 1
             
        # Decrement the end pointer till it finds an
        # element less than pivot
        while array[end] > pivot:
            end -= 1
         
        # If start and end have not crossed each other,
        # swap the numbers on start and end
        if(start < end):
            array[start], array[end] = array[end], array[start]
     
    # Swap pivot element with element on end pointer.
    # This puts pivot on its correct sorted place.
    array[end], array[pivot_index] = array[pivot_index], array[end]
    
    # Returning end pointer to divide the array into 2
    return end
     
# The main function that implements QuickSort
def quick_sort(start, end, array):
     
    if (start < end):
         
        # p is partitioning index, array[p]
        # is at right place
        p = partition(start, end, array)
         
        # Sort elements before partition
        # and after partition
        quick_sort(start, p - 1, array)
        quick_sort(p + 1, end, array)
         
# Driver code
array = [ 10, 7, 8, 9, 1, 5 ]
quick_sort(0, len(array) - 1, array)
 
print(f"Sorted array: {array}")
     
# This code is contributed by Adnan Aliakbar

Output

Sorted array: 
1 5 7 8 9 10

Анализ QuickSort
В общем, время, затраченное QuickSort, можно записать следующим образом.

 Т (п) = Т (к) + Т (нк-1) +  (п)

Первые два члена относятся к двум рекурсивным вызовам, последний термин - к процессу разделения. k - количество элементов, меньших, чем pivot.
Время, затрачиваемое QuickSort, зависит от входного массива и стратегии разделения. Ниже приведены три случая.

Худший случай: худший случай возникает, когда процесс разделения всегда выбирает наибольший или наименьший элемент в качестве опорного. Если мы рассмотрим вышеприведенную стратегию разделения, в которой последний элемент всегда выбирается в качестве опорного, худший случай будет иметь место, когда массив уже отсортирован в порядке возрастания или убывания. Ниже приводится повторение в худшем случае.

 Т (п) = Т (0) + Т (п-1) +  (п)
что эквивалентно  
Т (п) = Т (п-1) +  (п)

Решение вышеупомянутого повторения 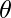(№ ² ).

Лучший случай: лучший случай возникает, когда процесс разделения всегда выбирает средний элемент в качестве опорного. Ниже приводится повторение в лучшем случае.

 Т (п) = 2Т (п / 2) +  (п)

Решение вышеупомянутого повторения 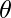(nLogn). Ее можно решить, используя случай 2 основной теоремы.

Средний случай:
Чтобы провести анализ среднего случая, нам нужно рассмотреть все возможные перестановки массива и вычислить время, затрачиваемое на каждую перестановку, что выглядит непросто.
Мы можем получить представление о среднем случае, рассматривая случай, когда раздел помещает O (n / 9) элементов в один набор и O (9n / 10) элементов в другой набор. Ниже приводится повторение этого случая.

 Т (п) = Т (п / 9) + Т (9 п / 10) +  (п)

Решение вышеуказанного повторения также O (nLogn)
Хотя в худшем случае временная сложность QuickSort составляет O (n ² ), что больше, чем у многих других алгоритмов сортировки, таких как сортировка слиянием и сортировка кучи, QuickSort на практике работает быстрее, потому что его внутренний цикл может быть эффективно реализован на большинстве архитектур и в большинстве данные из реального мира. QuickSort можно реализовать по-разному, изменив выбор точки поворота, так что худший случай редко встречается для данного типа данных. Однако сортировка слиянием обычно считается лучше, когда данные огромны и хранятся во внешнем хранилище.

QuickSort стабилен ?
Реализация по умолчанию нестабильна. Однако любой алгоритм сортировки можно сделать стабильным, если рассматривать индексы как параметр сравнения.

Быстрая сортировка на месте ?
Согласно широкому определению алгоритма на месте он квалифицируется как алгоритм сортировки на месте, поскольку он использует дополнительное пространство только для хранения рекурсивных вызовов функций, но не для управления вводом.

Что такое 3-сторонняя быстрая сортировка?
В простом алгоритме QuickSort мы выбираем элемент в качестве стержня, разбиваем массив вокруг стержня и повторяем для подмассивов слева и справа от стержня.
Рассмотрим массив, в котором много повторяющихся элементов. Например, {1, 4, 2, 4, 2, 4, 1, 2, 4, 1, 2, 2, 2, 2, 4, 1, 4, 4, 4}. Если 4 выбрано в качестве опорной точки в Simple QuickSort, мы исправляем только одно 4 и рекурсивно обрабатываем оставшиеся вхождения. В 3 Way QuickSort массив arr [l..r] делится на 3 части:
a) arr [l..i] элементов меньше pivot.
б) arr [i + 1..j-1] элементов, равных pivot.
c) arr [j..r] элементов больше, чем pivot.
См. Это для реализации.

Как реализовать QuickSort для связанных списков?
Быстрая сортировка по односвязному списку
Быстрая сортировка по двусвязному списку

Можем ли мы реализовать QuickSort итеративно?
Да, см. Итеративная быстрая сортировка.

Почему быстрая сортировка предпочтительнее MergeSort для сортировки массивов
Быстрая сортировка в общем виде - это сортировка на месте (т.е. она не требует дополнительного хранилища), тогда как сортировка слиянием требует дополнительного хранилища O (N), N обозначает размер массива, что может быть довольно дорогостоящим. Выделение и освобождение дополнительного пространства, используемого для сортировки слиянием, увеличивает время работы алгоритма. Сравнивая среднюю сложность, мы обнаруживаем, что оба типа сортировки имеют среднюю сложность O (NlogN), но константы различаются. Для массивов сортировка слиянием проигрывает из-за использования дополнительного места для хранения O (N).
В большинстве практических реализаций быстрой сортировки используется рандомизированная версия. В рандомизированной версии ожидаемая временная сложность O (nLogn). Худший случай возможен и в рандомизированной версии, но худший случай не возникает для определенного шаблона (например, отсортированного массива), и рандомизированная быстрая сортировка хорошо работает на практике.
Быстрая сортировка также является удобным для кеша алгоритмом сортировки, поскольку при использовании для массивов имеет хорошую локальность ссылки.
Быстрая сортировка также является хвостовой рекурсивной, поэтому выполняется оптимизация хвостового вызова.

Почему MergeSort предпочтительнее QuickSort для связанных списков?
В случае связанных списков дело обстоит иначе, в основном из-за разницы в распределении памяти для массивов и связанных списков. В отличие от массивов, узлы связанного списка не могут быть смежными в памяти. В отличие от массива, в связанном списке мы можем вставлять элементы посередине за O (1) дополнительное пространство и O (1) время. Поэтому операцию слияния сортировки слиянием можно реализовать без дополнительного места для связанных списков.
В массивах мы можем выполнять произвольный доступ, поскольку элементы непрерывны в памяти. Допустим, у нас есть целочисленный (4-байтовый) массив A, и пусть адрес A [0] равен x, тогда для доступа к A [i] мы можем напрямую получить доступ к памяти по адресу (x + i * 4). В отличие от массивов, мы не можем делать произвольный доступ в связанном списке. Быстрая сортировка требует большого количества такого доступа. В связанном списке для доступа к i-му индексу мы должны перемещаться по каждому узлу от головы до i-го узла, поскольку у нас нет непрерывного блока памяти. Следовательно, для быстрой сортировки накладные расходы увеличиваются. Сортировка слиянием обеспечивает доступ к данным последовательно, и потребность в произвольном доступе невелика.

Как оптимизировать QuickSort, чтобы в худшем случае он занимал O (Log n) лишнего места?
См. Раздел Оптимизация хвостового вызова QuickSort (уменьшение пространства для журнала в худшем случае)
https://youtu.be/PgBzjlCcFvc

Снимки:

Викторина по QuickSort
Последние статьи о QuickSort
Практика кодирования для сортировки.

Использованная литература:
http://en.wikipedia.org/wiki/Quicksort

Другие алгоритмы сортировки на GeeksforGeeks / GeeksQuiz:
Сортировка по выбору, пузырьковая сортировка, сортировка вставкой, сортировка слиянием, сортировка по куче, быстрая сортировка, радикальная сортировка, подсчетная сортировка, сортировка по ведру, сортировка по оболочке, сортировка по гребенке, сортировка по голубям
Пожалуйста, напишите комментарии, если вы обнаружите что-то неправильное, или вы хотите поделиться дополнительной информацией по теме, обсужденной выше.

QuickSort

C++14

Java

Python3

РЕКОМЕНДУЕМЫЕ СТАТЬИ