Прямая и обратная интерполяция Ньютона
Опубликовано: 18 Января, 2022
Интерполяция - это метод оценки значения функции для любого промежуточного значения независимой переменной, в то время как процесс вычисления значения функции вне заданного диапазона называется экстраполяцией .
Прямые разности : разности y1 - y0, y2 - y1, y3 - y2, ……, yn - yn – 1, когда обозначаются dy0, dy1, dy2, ……, dyn – 1, соответственно, называются первыми прямыми разностями. Таким образом, первые прямые отличия: 
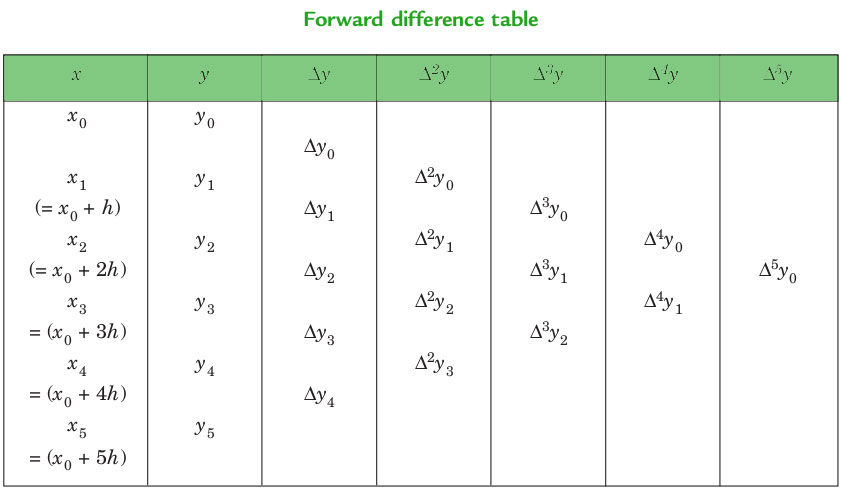
ФОРМУЛА ИНТЕРПОЛЯЦИИ ГРЕГОРИ НЬЮТОНА : 
Эта формула особенно полезна для интерполяции значений f (x) около начала заданного набора значений. h называется интервалом разности и u = (x - a) / h , здесь a - первое слагаемое.
Пример :
Input : Value of Sin 52

Выход :
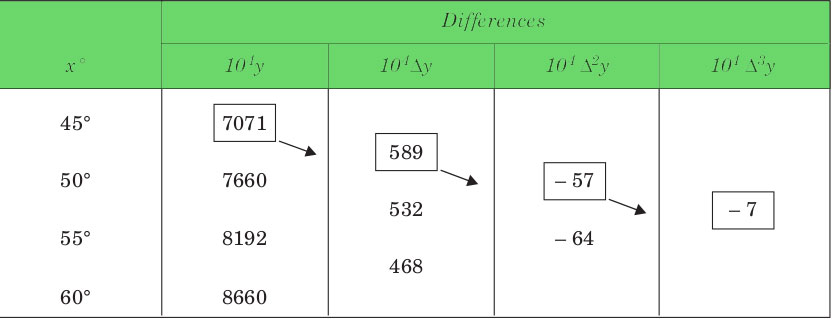
Значение Sin 52 составляет 0,788003.
Below is the implementation of the Newton forward interpolation method.
C++
// CPP Program to interpolate using// newton forward interpolation#include <bits/stdc++.h>using namespace std;// calculating u mentioned in the formulafloat u_cal(float u, int n){ float temp = u; for (int i = 1; i < n; i++) temp = temp * (u - i); return temp;}// calculating factorial of given number nint fact(int n){ int f = 1; for (int i = 2; i <= n; i++) f *= i; return f;}int main(){ // Number of values given int n = 4; float x[] = { 45, 50, 55, 60 }; // y[][] is used for difference table // with y[][0] used for input float y[n][n]; y[0][0] = 0.7071; y[1][0] = 0.7660; y[2][0] = 0.8192; y[3][0] = 0.8660; // Calculating the forward difference // table for (int i = 1; i < n; i++) { for (int j = 0; j < n - i; j++) y[j][i] = y[j + 1][i - 1] - y[j][i - 1]; } // Displaying the forward difference table for (int i = 0; i < n; i++) { cout << setw(4) << x[i] << " "; for (int j = 0; j < n - i; j++) cout << setw(4) << y[i][j] << " "; cout << endl; } // Value to interpolate at float value = 52; // initializing u and sum float sum = y[0][0]; float u = (value - x[0]) / (x[1] - x[0]); for (int i = 1; i < n; i++) { sum = sum + (u_cal(u, i) * y[0][i]) / fact(i); } cout << "
Value at " << value << " is " << sum << endl; return 0;} |
Java
// Java Program to interpolate using// newton forward interpolationclass GFG{// calculating u mentioned in the formulastatic double u_cal(double u, int n){ double temp = u; for (int i = 1; i < n; i++) temp = temp * (u - i); return temp;}// calculating factorial of given number nstatic int fact(int n){ int f = 1; for (int i = 2; i <= n; i++) f *= i; return f;}public static void main(String[] args){ // Number of values given int n = 4; double x[] = { 45, 50, 55, 60 }; // y[][] is used for difference table // with y[][0] used for input double y[][]=new double[n][n]; y[0][0] = 0.7071; y[1][0] = 0.7660; y[2][0] = 0.8192; y[3][0] = 0.8660; // Calculating the forward difference // table for (int i = 1; i < n; i++) { for (int j = 0; j < n - i; j++) y[j][i] = y[j + 1][i - 1] - y[j][i - 1]; } // Displaying the forward difference table for (int i = 0; i < n; i++) { System.out.print(x[i]+" "); for (int j = 0; j < n - i; j++) System.out.print(y[i][j]+" "); System.out.println(); } // Value to interpolate at double value = 52; // initializing u and sum double sum = y[0][0]; double u = (value - x[0]) / (x[1] - x[0]); for (int i = 1; i < n; i++) { sum = sum + (u_cal(u, i) * y[0][i]) / fact(i); } System.out.println("
Value at "+value+" is "+String.format("%.6g%n",sum));}}// This code is contributed by mits |
Python3
# Python3 Program to interpolate using# newton forward interpolation# calculating u mentioned in the formuladef u_cal(u, n): temp = u; for i in range(1, n): temp = temp * (u - i); return temp;# calculating factorial of given number ndef fact(n): f = 1; for i in range(2, n + 1): f *= i; return f;# Driver Code# Number of values givenn = 4;x = [ 45, 50, 55, 60 ]; # y[][] is used for difference table# with y[][0] used for inputy = [[0 for i in range(n)] for j in range(n)];y[0][0] = 0.7071;y[1][0] = 0.7660;y[2][0] = 0.8192;y[3][0] = 0.8660;# Calculating the forward difference# tablefor i in range(1, n): for j in range(n - i): y[j][i] = y[j + 1][i - 1] - y[j][i - 1];# Displaying the forward difference tablefor i in range(n): print(x[i], end = " "); for j in range(n - i): print(y[i][j], end = " "); print("");# Value to interpolate atvalue = 52;# initializing u and sumsum = y[0][0];u = (value - x[0]) / (x[1] - x[0]);for i in range(1,n): sum = sum + (u_cal(u, i) * y[0][i]) / fact(i);print("
Value at", value, "is", round(sum, 6));# This code is contributed by mits |
C#
// C# Program to interpolate using// newton forward interpolationusing System;class GFG{// calculating u mentioned in the formulastatic double u_cal(double u, int n){ double temp = u; for (int i = 1; i < n; i++) temp = temp * (u - i); return temp;}// calculating factorial of given number nstatic int fact(int n){ int f = 1; for (int i = 2; i <= n; i++) f *= i; return f;}// Driver codepublic static void Main(){ // Number of values given int n = 4; double[] x = { 45, 50, 55, 60 }; // y[,] is used for difference table // with y[,0] used for input double[,] y=new double[n,n]; y[0,0] = 0.7071; y[1,0] = 0.7660; y[2,0] = 0.8192; y[3,0] = 0.8660; // Calculating the forward difference // table for (int i = 1; i < n; i++) { for (int j = 0; j < n - i; j++) y[j,i] = y[j + 1,i - 1] - y[j,i - 1]; } // Displaying the forward difference table for (int i = 0; i < n; i++) { Console.Write(x[i]+" "); for (int j = 0; j < n - i; j++) Console.Write(y[i,j]+" "); Console.WriteLine(); } // Value to interpolate at double value = 52; // initializing u and sum double sum = y[0,0]; double u = (value - x[0]) / (x[1] - x[0]); for (int i = 1; i < n; i++) { sum = sum + (u_cal(u, i) * y[0,i]) / fact(i); } Console.WriteLine("
Value at "+value+" is "+Math.Round(sum,6));}}// This code is contributed by mits |
PHP
<?php// PHP Program to interpolate using// newton forward interpolation// calculating u mentioned in the formulafunction u_cal($u, $n){ $temp = $u; for ($i = 1; $i < $n; $i++) $temp = $temp * ($u - $i); return $temp;}// calculating factorial of given number nfunction fact($n){ $f = 1; for ($i = 2; $i <= $n; $i++) $f *= $i; return $f;}// Driver Code// Number of values given$n = 4;$x = array( 45, 50, 55, 60 );// y[,] is used for difference table// with y[,0] used for input$y = array_fill(0, $n, array_fill(0, $n, 0));$y[0][0] = 0.7071;$y[1][0] = 0.7660;$y[2][0] = 0.8192;$y[3][0] = 0.8660;// Calculating the forward difference// tablefor ($i = 1; $i < $n; $i++){ for ($j = 0; $j < $n - $i; $j++) $y[$j][$i] = $y[$j + 1][$i - 1] - $y[$j][$i - 1];}// Displaying the forward difference tablefor ($i = 0; $i < $n; $i++){ print($x[$i] . " "); for ($j = 0; $j < $n - $i; $j++) print($y[$i][$j] . " "); print("
");}// Value to interpolate at$value = 52;// initializing u and sum$sum = $y[0][0];$u = ($value - $x[0]) / ($x[1] - $x[0]);for ($i = 1; $i < $n; $i++){ $sum = $sum + (u_cal($u, $i) * $y[0][$i]) / fact($i);}print("
Value at " . $value . " is " . round($sum, 6));// This code is contributed by mits |
Javascript
<script> // javascript Program to interpolate using // newton forward interpolation // calculating u mentioned in the formula function u_cal(u , n) { var temp = u; for (var i = 1; i < n; i++) temp = temp * (u - i); return temp; } // calculating factorial of given number n function fact(n) { var f = 1; for (var i = 2; i <= n; i++) f *= i; return f; } // Number of values given var n = 4; var x = [ 45, 50, 55, 60 ]; // y is used for difference table // with y[0] used for input var y=Array(n).fill(0.0).map(x => Array(n).fill(0.0));
|