Проверьте, соответствуют ли все элементы данного связанного списка нисходящему пути от любого узла в данном двоичном дереве.
Учитывая корень двоичного дерева и заголовок связанного списка, задача состоит в том, чтобы проверить, соответствуют ли все элементы связанного списка нисходящему пути от любого узла в данном двоичном дереве.
Примеры:
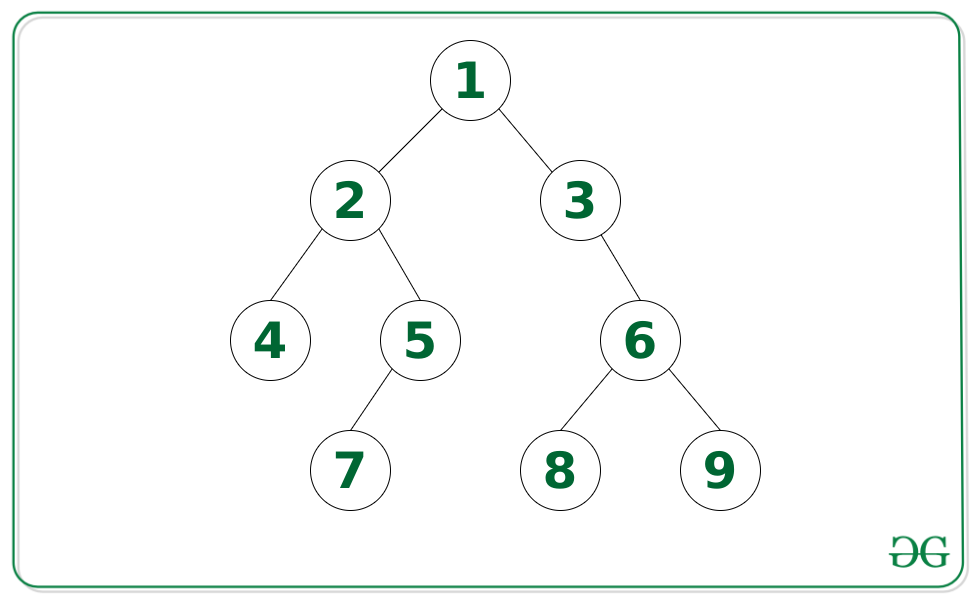
Input: Tree in the image below, list = {3, 6, 8}
Output: Yes
Explanation: There exists a downward path in the given Binary Tree, having all the elements of the linked list in the same order.Input: Tree in the image below, list = {1, 2, 5, 7}
Output: Yes
Подход: Данная проблема может быть решена с помощью DFS Traversal of the Binary tree. Во время обхода DFS, если какой-либо узел двоичного дерева равен заголовку связанного списка, можно вызвать рекурсивную функцию isPathUntil() , чтобы рекурсивно проверить, существуют ли другие элементы связанного списка как путь от этого узла. . Если полный связанный список был пройден, существует допустимый требуемый путь, поэтому верните true . В противном случае вернуть false . Выполните следующие шаги, чтобы решить данную проблему:
- Объявите функцию, скажем, isSubPathUtil(root, head) и выполните следующие шаги в этой функции:
- Если корень равен NULL , верните false .
- Если заголовок равен NULL, верните true.
- Если значение текущего корневого узла совпадает со значением текущего заголовка LL, то рекурсивно вызовите isSubPathUtil(root->left, head->next) и isSubPathUtil(root->right, head->next) и если значение, возвращенное одним из этих рекурсивных вызовов, равно true, то вернуть true. В противном случае вернуть false .
- Объявите функцию, скажем, isSubPath(root, head) и выполните следующие шаги в этой функции:
- Если корень равен NULL , верните false .
- Если заголовок равен NULL , верните true.
- Если значение текущего корневого узла совпадает со значением текущего заголовка LL, то рекурсивно вызовите isSubPath(root->left, head->next) и isSubPath(root->right, head->next) и если значение, возвращенное одним из этих рекурсивных вызовов, равно true, то вернуть true. В противном случае рекурсивно возвращайте значение для isSubPath(root->left, head) и isSubPath(root->right, head) .
- После вышеуказанных шагов, если значение, возвращаемое функцией isSubPath(root, head) , равно true , выведите Yes . В противном случае выведите Нет .
Ниже приведена реализация вышеуказанного подхода:
Временная сложность: O(N * M), где N = количество узлов в двоичном дереве и M = количество узлов в связанном списке.
Вспомогательное пространство: O(1)