Проверьте, находятся ли два числа в золотом сечении

Опубликовано: 10 Января, 2022

Учитывая два числа A и B , задача состоит в том, чтобы проверить, что A и B находятся в золотом сечении.
Золотое сечение: два числа считаются находящимися в золотом сечении, если их соотношение совпадает с отношением суммы двух чисел к большему числу. Здесь a> b> 0, Ниже представлено геометрическое представление золотого сечения:

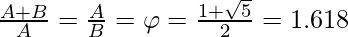
Примеры:

 Ввод: A = 1, B = 0,618.
Выход: Да
Объяснение:
Эти два числа вместе образуют золотое сечение.

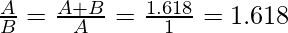
Input: A = 61.77, B = 38.22

Output Yes

Explanation:

These two numbers together forms Golden ratio

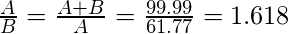
Рекомендуется: сначала попробуйте свой подход в {IDE}, прежде чем переходить к решению.

Подход: идея состоит в том, чтобы найти два отношения и проверить, что это соотношение равно золотому сечению. Это 1,618.

 // Здесь A обозначает большее число


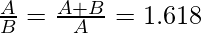
Below is the implementation of the above approach:

C++

// C++ implementation to check 
// whether two numbers are in 
// golden ratio with each other
#include <bits/stdc++.h>
using namespace std;
 
// Function to check that two 
// numbers are in golden ratio
bool checkGoldenRatio(float a,
                      float b)
{
  // Swapping the numbers such 
  // that A contains the maximum
  // number between these numbers
  if(a <= b)
  {
    float temp = a;
    a = b;
    b = temp;
  }
 
  // First Ratio
  std::stringstream ratio1;
  ratio1 << std :: fixed <<
            std :: setprecision(3) <<
            (a / b);
 
  // Second Ratio
  std::stringstream ratio2;
  ratio2 << std :: fixed <<
            std :: setprecision(3) <<
            (a + b) / a;
 
  // Condition to check that two
  // numbers are in golden ratio
  if((ratio1.str() == ratio2.str()) &&
      ratio1.str() == "1.618")
  {
    cout << "Yes" << endl;
    return true;
  }
  else
  {
    cout << "No" << endl;
    return false;
  }
}
  
// Driver code
int main()
{
  float a = 0.618;
  float b = 1;
 
  // Function Call
  checkGoldenRatio(a, b);
 
  return 0;
}
 
// This code is contributed by divyeshrabadiya07

Java

// Java implementation to check 
// whether two numbers are in 
// golden ratio with each other
class GFG{
     
// Function to check that two 
// numbers are in golden ratio
public static Boolean checkGoldenRatio(float a,
                                       float b)
{
     
    // Swapping the numbers such 
    // that A contains the maximum
    // number between these numbers
    if (a <= b)
    {
        float temp = a;
        a = b;
        b = temp;
    }
     
    // First Ratio
    String ratio1 = String.format("%.3f", a / b);
     
    // Second Ratio
    String ratio2 = String.format("%.3f", (a + b) / a);
     
    // Condition to check that two
    // numbers are in golden ratio
    if (ratio1.equals(ratio2) &&
        ratio1.equals("1.618"))
    {
        System.out.println("Yes");
        return true;
    }
    else
    {
        System.out.println("No");  
        return false;
    }
}
 
// Driver code
public static void main(String []args)
{
    float a = (float)0.618;
    float b = 1;
     
    // Function Call
    checkGoldenRatio(a, b);
}
}
 
// This code is contributed by rag2127

Python3

# Python3 implementation to check
# whether two numbers are in
# golden ratio with each other
 
# Function to check that two
# numbers are in golden ratio
def checkGoldenRatio(a, b):
     
    # Swapping the numbers such
    # that A contains the maximum
    # number between these numbers
    a, b = max(a, b), min(a, b)
     
    # First Ratio
    ratio1 = round(a/b, 3)
     
    # Second Ratio
    ratio2 = round((a+b)/a, 3)
    # Condition to check that two
    # numbers are in golden ratio
    if ratio1 == ratio2 and
       ratio1 == 1.618:
        print("Yes")
        return True
    else:
        print("No")
        return False
         
# Driver Code
if __name__ == "__main__":
    a = 0.618
    b = 1
     
    # Function Call
    checkGoldenRatio(a, b)

C#

// C# implementation to check 
// whether two numbers are in 
// golden ratio with each other
using System;
using System.Collections.Generic;
class GFG {
     
    // Function to check that two 
    // numbers are in golden ratio
    static bool checkGoldenRatio(float a,
                          float b)
    {
      // Swapping the numbers such 
      // that A contains the maximum
      // number between these numbers
      if(a <= b)
      {
        float temp = a;
        a = b;
        b = temp;
      }
      
      // First Ratio
      string ratio1 = String.Format("{0:0.000}", a / b);
      
      // Second Ratio
      string ratio2 = String.Format("{0:0.000}", (a + b) / a);
 
      // Condition to check that two
      // numbers are in golden ratio
      if(ratio1 == ratio2 && ratio1 == "1.618")
      {
        Console.WriteLine("Yes");
        return true;
      }
      else
      {
        Console.WriteLine("No");
        return false;
      }
    }
   
  // Driver code 
  static void Main() {
      float a = (float)0.618;
      float b = 1;
      
      // Function Call
      checkGoldenRatio(a, b);
  }
}
 
// This code is contributed by divyesh072019

Javascript

<script>
 
// Javascript implementation to check
// whether two numbers are in
// golden ratio with each other
 
// Function to check that two
// numbers are in golden ratio
function checkGoldenRatio(a, b)
{
      
    // Swapping the numbers such
    // that A contains the maximum
    // number between these numbers
    if (a <= b)
    {
        let temp = a;
        a = b;
        b = temp;
    }
      
    // First Ratio
    let ratio1 = (a / b).toFixed(3);
      
    // Second Ratio
    let ratio2 = ((a + b) / a).toFixed(3);
      
    // Condition to check that two
    // numbers are in golden ratio
    if ((ratio1 == ratio2) &&
        ratio1 == "1.618")
    {
        document.write("Yes");
        return true;
    }
    else
    {
        document.write("No"); 
        return false;
    }
}
 
// Driver Code
     
    let a = 0.618;
    let b = 1;
      
    // Function Call
    checkGoldenRatio(a, b);
 
</script>
Output: 
Yes

 

Ссылки: https://en.wikipedia.org/wiki/Golden_ratio

Вниманию читателя! Не прекращайте учиться сейчас. Получите все важные математические концепции для соревновательного программирования с курсом Essential Maths for CP по доступной для студентов цене. Чтобы завершить подготовку от изучения языка к DS Algo и многому другому, см. Полный курс подготовки к собеседованию .

РЕКОМЕНДУЕМЫЕ СТАТЬИ