Проверить, может ли число быть представлено в виде суммы двух положительных совершенных биквадратов

Для данного положительного целого числа N задача состоит в том, чтобы проверить, может ли N быть записано как сумма двух совершенных биквадратов или нет, то есть (N = X ⁴ + Y ⁴ ), где X и Y — целые неотрицательные числа . Если это возможно, то выведите Yes . В противном случае выведите Нет .

Примеры:

Input: N = 97
Output: Yes
Explanation: Summation of the biquadrates of 2 and 3 is 97, i.e. 2⁴ + 3⁴ = 16 + 81 = 97(= N).

Input: N = 7857
Output: Yes

Наивный подход: самый простой подход к решению данной проблемы состоит в том, чтобы рассмотреть все возможные комбинации целых чисел X и Y и проверить, равна ли сумма их биквадратов N или нет. Если найдено верно, то выведите Yes . В противном случае выведите Нет .

Временная сложность: O(sqrt(N))
Вспомогательное пространство: O(1)

Эффективный подход. Описанный выше подход также можно оптимизировать, используя подход с двумя указателями, идея которого состоит в том, чтобы найти два числа в диапазоне. 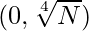. Выполните следующий шаг, чтобы решить эту проблему:

• Инициализируйте два указателя, скажем, i как 0 и j как .
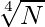• Повторяйте цикл до тех пор, пока j не станет меньше i , и выполните следующие шаги:
  • Если значение j ⁴ равно N и i ⁴ равно N , то выведите Yes .
  • Если значение (i ⁴ + i ⁴ ) или (j ⁴ + j ⁴ ) или (i ⁴ + j ⁴ ) равно N , то выведите Yes .
  • Если значение (i ⁴ + j ⁴ ) меньше N , то увеличивается указатель i на 1 . В противном случае уменьшите указатель j на 1 .
• Если после выполнения вышеуказанных шагов циклы обрываются, то выведите No , так как таких пар, удовлетворяющих заданным критериям, не существует.

Ниже приведена реализация вышеуказанного подхода:

Сложность времени: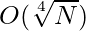
Вспомогательное пространство: O(1)