Программа для проверки сходства заданных двух треугольников
Опубликовано: 16 Января, 2022
Даны четыре массива из 3 чисел в каждом, которые представляют стороны и углы двух треугольников. Задача - проверить, похожи ли два треугольника или нет. Если это похоже, выведите теорему, по которой это так.
Примеры:
Ввод: сторона1 = [2, 3, 3] угол1 = [80, 60, 40]
сторона2 = [4, 6, 6] угол2 = [40, 60, 80]
Вывод: Треугольники похожи на SSS AAA SAS
Ввод: сторона1 = [2, 3, 4] угол1 = [85, 45, 50]
сторона2 = [4, 6, 6] угол2 = [40, 60, 80]
Вывод: треугольники не похожиРекомендуется: сначала попробуйте свой подход в {IDE}, прежде чем переходить к решению.
Подобные треугольники - это два или более треугольника, у которых все соответствующие углы равны, а все соответствующие стороны пропорциональны. Неважно, в каком направлении обращены треугольники. Их размер не имеет значения, если каждая сторона пропорциональна. Подобие треугольников доказывается следующими теоремами:
- Критерии сходства Side-Side-Side (SSS):
Если все стороны треугольника пропорциональны соответствующим сторонам другого треугольника, то треугольники называются подобными по свойству сторона-сторона-сторона (SSS).
В треугольнике ABC и PQR if треугольники AB / PQ = BC / QR = CA / RP подобны.

- Критерии подобия Side-Angle-Side (SAS):
Если две стороны двух треугольников пропорциональны и угол между ними одинаков в обоих треугольниках, то говорят, что треугольники похожи по свойству Side-Angle-Side (SAS).
В треугольнике ABC и PQR, если AB / PQ = BC / QR и знак равно
знак равно  треугольники похожи.
треугольники похожи.
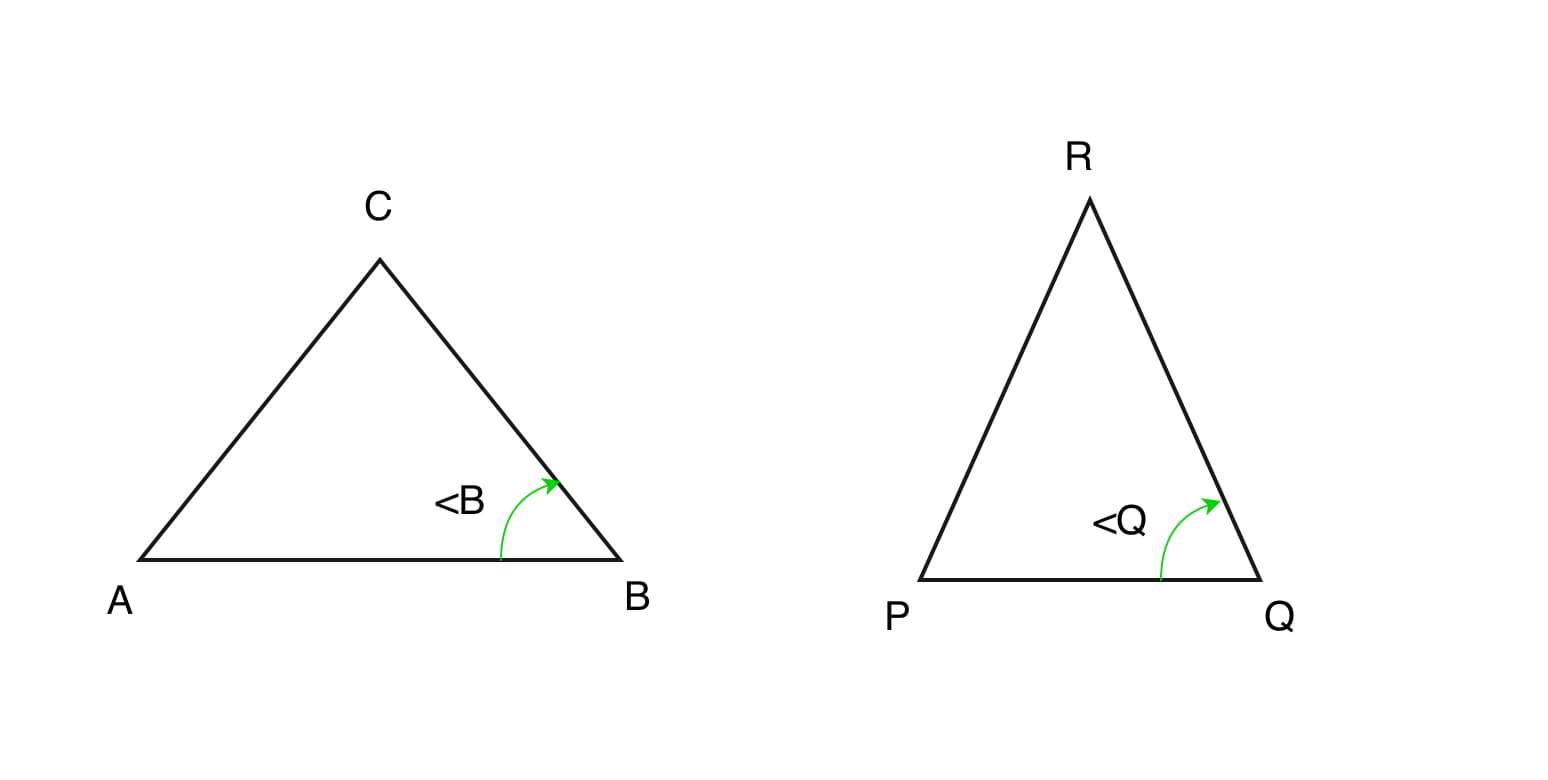
- Критерии подобия угол-угол-угол (AAA):
Если все углы треугольника равны соответствующим углам другого треугольника, то треугольники называются подобными по свойству Угол-Угол-Угол (AAA).
В треугольнике ABC и PQR, если знак равно
знак равно  ,
,  знак равно
знак равно  а также
а также  знак равно
знак равно  то треугольники похожи.
то треугольники похожи.

Below is the implementation of the above approach:
C++
// C++ program to check// similarity between// two triangles.#include<bits/stdc++.h>using namespace std;//Function for AAA similarityint simi_aaa(int a1[], int a2[]){ sort(a1, a1 + 3); sort(a2, a2 + 3); // Check for AAA if (a1[0] == a2[0] && a1[1] == a2[1] && a1[2] == a2[2]) return 1; else return 0; }// Function for// SAS similarityint simi_sas(int s1[], int s2[], int a1[], int a2[]){ sort(a1, a1 + 3); sort(a2, a2 + 3); sort(s1, s1 + 3); sort(s2, s2 + 3); // Check for SAS // angle b / w two smallest // sides is largest. if( s1[0] / s2[0] == s1[1] / s2[1]) { // since we take angle // b / w the sides. if (a1[2] == a2[2]) return 1; } if (s1[1] / s2[1] == s1[2] / s2[2]) { if (a1[0] == a2[0]) return 1; } if (s1[2] / s2[2] == s1[0] / s2[0]) { if(a1[1] == a2[1]) return 1; } return 0;}// Function for SSS similarityint simi_sss(int s1[], int s2[]){ sort(s1, s1 + 3); sort(s2, s2 + 3); // Check for SSS if(s1[0] / s2[0] == s1[1] / s2[1] && s1[1] / s2[1] == s1[2] / s2[2] && s1[2] / s2[2] == s1[0] / s2[0]) return 1; return 0;}// Driver Codeint main(){ int s1[] = {2, 3, 3}; int s2[] = {4, 6, 6}; int a1[] = {80, 60, 40}; int a2[] = {40, 60, 80}; // function call for // AAA similarity int aaa = simi_aaa(a1, a2); // function call for // SSS similarity int sss = simi_sss(s1, s2) ; // function call for // SAS similarity int sas = simi_sas(s1, s2, a1, a2) ; // Check if triangles // are similar or not if(aaa == 1 || sss == 1 || sas == 1) { cout << "Triangles are " << "similar by "; if(aaa == 1) cout << "AAA "; if(sss == 1) cout << "SSS "; if(sas == 1) cout << "SAS."; } else cout << "Triangles are " << "not similar"; return 0;}// This code is contributed// by Arnab Kundu |
Java
// Java program to check// similarity between// two triangles.import java.util.*;class GFG1{ // Function for// AAA similaritystatic int simi_aaa(int a1[], int a2[]){ Arrays.sort(a1); Arrays.sort(a2); // Check for AAA if (a1[0] == a2[0] && a1[1] == a2[1] && a1[2] == a2[2]) return 1; else return 0; }// Function for// SAS similaritystatic int simi_sas(int s1[], int s2[], int a1[], int a2[]){ Arrays.sort(a1); Arrays.sort(a2); Arrays.sort(s1); Arrays.sort(s2); // Check for SAS // angle b / w two smallest // sides is largest. if(s1[0] / s2[0] == s1[1] / s2[1]) { // since we take angle // b / w the sides. if (a1[2] == a2[2]) return 1; } if (s1[1] / s2[1] == s1[2] / s2[2]) { if (a1[0] == a2[0]) return 1; } if (s1[2] / s2[2] == s1[0] / s2[0]) { if(a1[1] == a2[1]) return 1; } return 0;}// Function for// SSS similaritystatic int simi_sss(int s1[], int s2[]){ Arrays.sort(s1); Arrays.sort(s2); // Check for SSS if(s1[0] / s2[0] == s1[1] / s2[1] && s1[1] / s2[1] == s1[2] / s2[2] && s1[2] / s2[2] == s1[0] / s2[0]) return 1; return 0;}// Driver Codepublic static void main(String args[]){ int s1[] = {2, 3, 3}; int s2[] = {4, 6, 6}; int a1[] = {80, 60, 40}; int a2[] = {40, 60, 80}; // function call for // AAA similarity int aaa = simi_aaa(a1, a2); // function call for // SSS similarity int sss = simi_sss(s1, s2) ; // function call for // SAS similarity int sas = simi_sas(s1, s2, a1, a2) ; // Check if triangles // are similar or not if(aaa == 1 || sss == 1 || sas == 1) { System.out.print("Triangles are " + "similar by "); if(aaa == 1) System.out.print("AAA "); if(sss == 1) System.out.print("SSS "); if(sas == 1) System.out.print("SAS."); } else System.out.println("Triangles are " + "not similar");}}// This code is contributed// by Arnab Kundu |
Python
# Python program to check# similarity between two triangles.# Function for AAA similaritydef simi_aaa(a1, a2): a1 = [float(i) for i in a1] a2 = [float(i) for i in a2] a1.sort() a2.sort() # Check for AAA if a1[0] == a2[0] and a1[1] == a2[1] and a1[2] == a2[2]: return 1 return 0# Function for SAS similaritydef simi_sas(s1, s2, a1, a2): s1 = [float(i) for i in s1] s2 = [float(i) for i in s2] a1 = [float(i) for i in a1] a2 = [float(i) for i in a2] s1.sort() s2.sort() a1.sort() a2.sort() # Check for SAS # angle b / w two smallest sides is largest. if s1[0] / s2[0] == s1[1] / s2[1]: # since we take angle b / w the sides. if a1[2] == a2[2]: return 1 if s1[1] / s2[1] == s1[2] / s2[2]: if a1[0] == a2[0]: return 1 if s1[2] / s2[2] == s1[0] / s2[0]: if a1[1] == a2[1]: return 1 return 0# Function for SSS similaritydef simi_sss(s1, s2): s1 = [float(i) for i in s1] s2 = [float(i) for i in s2] s1.sort() s2.sort() # Check for SSS if(s1[0] / s2[0] == s1[1] / s2[1] and s1[1] / s2[1] == s1[2] / s2[2] and s1[2] / s2[2] == s1[0] / s2[0]): return 1 return 0 # Driver Codes1 = [2, 3, 3]s2 = [4, 6, 6] a1 = [80, 60, 40]a2 = [40, 60, 80]# function call for AAA similarityaaa = simi_aaa(a1, a2)# function call for SSS similaritysss = simi_sss(s1, s2)# function call for SAS similaritysas = simi_sas(s1, s2, a1, a2)# Check if triangles are similar or notif aaa or sss or sas: print "Triangles are similar by", if aaa: print "AAA", if sss: print "SSS", if sas: print "SAS"else: print "Triangles are not similar" |
C#
// C# program to check// similarity between// two triangles.using System;class GFG1{ // Function for// AAA similaritystatic int simi_aaa(int [] a1, int [] a2){ Array.Sort(a1); Array.Sort(a2); // Check for AAA if (a1[0] == a2[0] && a1[1] == a2[1] &&РЕКОМЕНДУЕМЫЕ СТАТЬИ |