Программа для поиска площади треугольника

Опубликовано: 21 Января, 2022

Нахождение области по заданным сторонам:

Примеры :

 Ввод: a = 5, b = 7, c = 8
Выход: Площадь треугольника 17,320508


Ввод: a = 3, b = 4, c = 5
Выход: Площадь треугольника 6,000000.

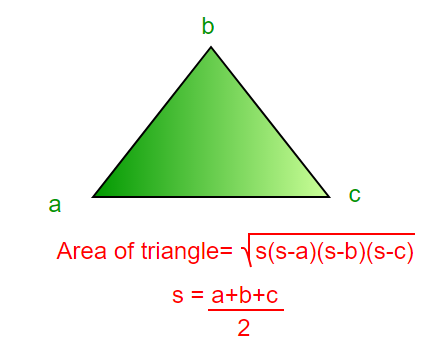
Площадь треугольника можно просто оценить по следующей формуле.

 Площадь = sqrt (s * (sa) * (sb) * (sc))
где a, b и c - длины сторон
треугольник и s = (a + b + c) / 2

Рекомендуется: сначала решите эту проблему на «ПРАКТИКЕ», прежде чем переходить к решению.

 

C++

// C++ Program to find the area
// of triangle
#include <bits/stdc++.h>
using namespace std;
 
float findArea(float a, float b, float c)
{
    // Length of sides must be positive
    // and sum of any two sides
    // must be smaller than third side.
    if (a < 0 || b < 0 || c < 0 ||
       (a + b <= c) || a + c <= b ||
                       b + c <= a)
    {
        cout << "Not a valid trianglen";
        exit(0);
    }
    float s = (a + b + c) / 2;
    return sqrt(s * (s - a) *
                    (s - b) * (s - c));
}
 
// Driver Code
int main()
{
    float a = 3.0;
    float b = 4.0;
    float c = 5.0;
 
    cout << "Area is " << findArea(a, b, c);
    return 0;
}
 
// This code is contributed
// by rathbhupendra

C

#include <stdio.h>
#include <stdlib.h>
 
float findArea(float a, float b, float c)
{
    // Length of sides must be positive and sum of any two sides
    // must be smaller than third side.
    if (a < 0 || b < 0 || c <0 || (a+b <= c) ||
        a+c <=b || b+c <=a)
    {
        printf("Not a valid trianglen");
        exit(0);
    }
    float s = (a+b+c)/2;
    return sqrt(s*(s-a)*(s-b)*(s-c));
}
 
int main()
{
    float a = 3.0;
    float b = 4.0;
    float c = 5.0;
 
    printf("Area is %f", findArea(a, b, c));
    return 0;
}

Java

// Java program to print
// Floyd"s triangle
     
class Test
{
    static float findArea(float a, float b, float c)
    {
        // Length of sides must be positive and sum of any two sides
        // must be smaller than third side.
        if (a < 0 || b < 0 || c <0 || (a+b <= c) ||
            a+c <=b || b+c <=a)
        {
            System.out.println("Not a valid triangle");
            System.exit(0);
        }
        float s = (a+b+c)/2;
        return (float)Math.sqrt(s*(s-a)*(s-b)*(s-c));
    }
         
    // Driver method
    public static void main(String[] args)
    {
        float a = 3.0f;
        float b = 4.0f;
        float c = 5.0f;
     
        System.out.println("Area is " + findArea(a, b, c));
    }
}

Python

# Python Program to find the area
# of triangle
 
# Length of sides must be positive
# and sum of any two sides
def findArea(a,b,c):
 
    # must be smaller than third side.
    if (a < 0 or b < 0 or c < 0 or (a+b <= c) or (a+c <=b) or (b+c <=a) ):
        print("Not a valid trianglen")
        return
         
    # calculate the semi-perimeter
    s = (a + b + c) / 2
     
    # calculate the area
    area = (s * (s - a) * (s - b) * (s - c)) ** 0.5
    print("Area of a traingle is %f" %area)
 
 
# Initialize first side of traingle
a = 3.0
# Initialize second side of traingle
b = 4.0
# Initialize Third side of traingle
c = 5.0
findArea(a,b,c)
 
# This code is contributed by Shariq Raza

C#

// C# program to print
// Floyd"s triangle
using System;
 
class Test {
     
    // Function to find area
    static float findArea(float a, float b,
                        float c)
    {
         
        // Length of sides must be positive
        // and sum of any two sides
        // must be smaller than third side.
        if (a < 0 || b < 0 || c <0 ||
        (a + b <= c) || a + c <=b ||
            b + c <=a)
        {
            Console.Write("Not a valid triangle");
            System.Environment.Exit(0);
        }
        float s = (a + b + c) / 2;
        return (float)Math.Sqrt(s * (s - a) *
                            (s - b) * (s - c));
    }
         
    // Driver code
    public static void Main()
    {
        float a = 3.0f;
        float b = 4.0f;
        float c = 5.0f;
     
        Console.Write("Area is " + findArea(a, b, c));
    }
}
 
// This code is contributed Nitin Mittal.

PHP

<?php
function findArea($a, $b, $c)
{
    // Length of sides must be positive
    // and sum of any two sides must
    // be smaller than third side.
    if ($a < 0 or $b < 0 or
        $c < 0 or ($a + $b <= $c) or
        $a + $c <= $b or $b + $c <= $a)
    {
        echo "Not a valid trianglen";
        exit(0);
    }
    $s = ($a + $b + $c) / 2;
    return sqrt($s * ($s - $a) *
            ($s - $b) * ($s - $c));
}
 
// Driver Code
$a = 3.0;
$b = 4.0;
$c = 5.0;
 
echo "Area is ", findArea($a, $b, $c);
 
// This code is contributed anuJ_67.
?>

Javascript

<script>
 
// javascript Program to find the area
// of triangle
 
function findArea( a,  b,  c)
{
    // Length of sides must be positive
    // and sum of any two sides
    // must be smaller than third side.
    if (a < 0 || b < 0 || c < 0 ||
       (a + b <= c) || a + c <= b ||
                       b + c <= a)
    {
        document.write( "Not a valid trianglen");
        return;
    }
    let s = (a + b + c) / 2;
    return Math.sqrt(s * (s - a) *
                    (s - b) * (s - c));
}
 
// Driver Code
 
    let a = 3.0;
    let b = 4.0;
    let c = 5.0;
 
  document.write( "Area is " + findArea(a, b, c));
 
// This code is contributed by todaysgaurav
 
</script>

Выход :

 Площадь 6

Нахождение района по координатам:

Если нам даны координаты трех углов, мы можем применить приведенную ниже формулу Шнурка для площади.

 Площадь

= | 1/2 [(x 1 y 2 + x 2 y 3 + ... + x n-1 y n + x n y 1 ) -
(x 2 y 1 + x 3 y 2 + ... + x n y n-1 + x 1 y n )] |

 

C++

// C++ program to evaluate area of a polygon using
// shoelace formula
#include <bits/stdc++.h>
using namespace std;
  
// (X[i], Y[i]) are coordinates of i"th point.
double polygonArea(double X[], double Y[], int n)
{
    // Initialize area
    double area = 0.0;
  
    // Calculate value of shoelace formula
    int j = n - 1;
    for (int i = 0; i < n; i++)
    {
        area += (X[j] + X[i]) * (Y[j] - Y[i]);
        j = i;  // j is previous vertex to i
    }
  
    // Return absolute value
    return abs(area / 2.0);
}
  
// Driver program to test above function
int main()
{
    double X[] = {0, 2, 4};
    double Y[] = {1, 3, 7};
  
    int n = sizeof(X)/sizeof(X[0]);
  
    cout << polygonArea(X, Y, n);
}

Java

// Java program to evaluate area of
// a polygon usingshoelace formula
import java.io.*;
import java.math.*;
 
class GFG {
 
    // (X[i], Y[i]) are coordinates of i"th point.
    static double polygonArea(double X[], double Y[], int n)
    {
        // Initialize area
        double area = 0.0;
     
        // Calculate value of shoelace formula
        int j = n - 1;
        for (int i = 0; i < n; i++)
        {
            area += (X[j] + X[i]) * (Y[j] - Y[i]);
             
            // j is previous vertex to i
            j = i;
        }
     
        // Return absolute value
        return Math.abs(area / 2.0);
    }
     
    // Driver program
    public static void main (String[] args)
    {
        double X[] = {0, 2, 4};
        double Y[] = {1, 3, 7};
 
        int n = X.length;
        System.out.println(polygonArea(X, Y, n));
    }
}
 
 
// This code is contributed
// by Nikita Tiwari.

Python3

# Python 3 program to evaluate
# area of a polygon using
# shoelace formula
 
# (X[i], Y[i]) are coordinates of i"th point.
def polygonArea(X,Y, n) :
 
    # Initialize area
    area = 0.0
   
    # Calculate value of shoelace formula
    j = n - 1
    for i in range( 0, n) :
        area = area + (X[j] + X[i]) * (Y[j] - Y[i])
        j = i  # j is previous vertex to i
     
     
    # Return absolute value
    return abs(area // 2.0)
 
   
# Driver program to test above function
X = [0, 2, 4]
Y = [1, 3, 7]
 
n = len(X)
print(polygonArea(X, Y, n))
 
 
# This code is contributed
# by Nikita Tiwari.

C#

// C# program to evaluate area of
// a polygon usingshoelace formula
using System;
 
class GFG {
 
    // (X[i], Y[i]) are coordinates
    // of i"th point.
    static double polygonArea(double []X,
                       double []Y, int n)
    {
        // Initialize area
        double area = 0.0;
     
        // Calculate value of shoelace
        // formula
        int j = n - 1;
        for (int i = 0; i < n; i++)
        {
            area += (X[j] + X[i]) *
                        (Y[j] - Y[i]);
             
            // j is previous vertex to i
            j = i;
        }
     
        // Return absolute value
        return Math.Abs(area / 2.0);
    }
     
    // Driver program
    public static void Main ()
    {
        double []X = {0, 2, 4};
        double []Y = {1, 3, 7};
 
        int n = X.Length;
        Console.WriteLine(
                 polygonArea(X, Y, n));
    }
}
 
// This code is contributed by anuj_67.

PHP

<?php
// PHP program to evaluate area of a
// polygon using shoelace formula
 
// (X[i], Y[i]) are coordinates
// of i"th point.
function polygonArea( $X, $Y, $n)
{
     
    // Initialize area
    $area = 0.0;
 
Школьное программирование

РЕКОМЕНДУЕМЫЕ СТАТЬИ

Количество чисел между L и R, взаимно простых с P
27 Февраля, 2023
Максимизируйте число из заданных целых чисел, используя следующие операции
27 Февраля, 2023
Максимизируйте частоту элемента, добавив X в подпоследовательность
26 Февраля, 2023
Элемент поиска в матрице
26 Февраля, 2023
Минимизируйте вставку 0 или 1, чтобы ни одна соседняя пара не имела одинакового значения
25 Февраля, 2023
XOR всех элементов массива, которые являются идеальными квадратами
25 Февраля, 2023
Найдите минимум конфет, оставшихся после соблюдения заданных правил.
25 Февраля, 2023
Проверьте, можно ли создать массив со средним значением X, используя N элементов данного массива.
23 Февраля, 2023