Программа для поиска центра треугольника

Опубликовано: 13 Января, 2022

Даны вершины треугольника и длины его сторон. В треугольник вписан круг. Задача - найти центр треугольника.
Примеры:

 Ввод: A (2, 2), B (1, 1), C (3, 1) 
        и AB = 2, BC = 1, AC = 1
Выход: (2, 1.5)

Ввод: A (3, 3), B (1, 2), C (2, 2) 
        и AB = 3, BC = 2, AC = 2
Выход: (2,5, 2,83)

Рекомендуется: сначала попробуйте свой подход в {IDE}, прежде чем переходить к решению.

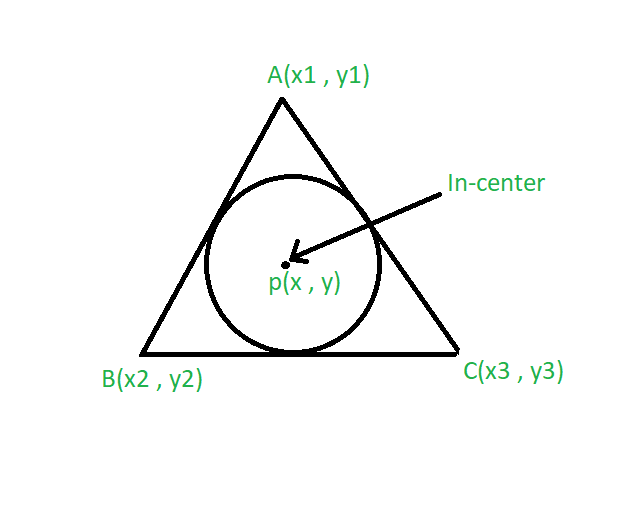
Подход:

Центр круга, касающийся сторон треугольника, называется его центром.
Предположим, что вершины треугольника - это A (x1, y1), B (x2, y2) и C (x3, y3).
Пусть сторона AB = a, BC = b, AC = c, тогда координаты центра задаются формулой:

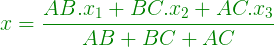
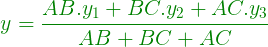
Below is the implementation of the above approach:

C++

// C++ program to find the
// incenter of a triangle
#include <bits/stdc++.h>
using namespace std;
 
// Driver code
int main()
{
    // coordinate of the vertices
    float x1 = 2, x2 = 1, x3 = 3;
    float y1 = 2, y2 = 1, y3 = 1;
    float a = 2, b = 1, c = 1;
 
    // Formula to calculate in-center
    float x = (a * x1 + b *
                   x2 + c * x3) / (a + b + c);
    float y = (a * y1 + b *
                   y2 + c * y3) / (a + b + c);
 
    // System.out.print(setprecision(3));
    cout << "Incenter = "
         << "(" << x << ", " << y << ")";
    return 0;
}
 
// This code is contributed by 29AjayKumar

Java

// Java program to find the
// incenter of a triangle
 
import java.util.*;
import java.lang.*;
 
class GFG {
 
    // Driver code
    public static void main(String args[])
    {
        // coordinate of the vertices
        float x1 = 2, x2 = 1, x3 = 3;
        float y1 = 2, y2 = 1, y3 = 1;
        float a = 2, b = 1, c = 1;
 
        // Formula to calculate in-center
        float x
            = (a * x1 + b * x2 + c * x3) / (a + b + c);
        float y
            = (a * y1 + b * y2 + c * y3) / (a + b + c);
 
        // System.out.print(setprecision(3));
        System.out.println("Incenter= "
                           + "(" + x + ", " + y + ")");
    }
}

Python3

# Python3 program to find the
# incenter of a triangle
 
# Driver code
 
# coordinate of the vertices
x1 = 2; x2 = 1; x3 = 3;
y1 = 2; y2 = 1; y3 = 1;
a = 2; b = 1; c = 1;
 
# Formula to calculate in-center
x = (a * x1 + b * x2 + c * x3) / (a + b + c);
y = (a * y1 + b * y2 + c * y3) / (a + b + c);
 
# System.out.print(setprecision(3));
print("Incenter = (", x, ",", y, ")");
 
# This code is contributed
# by Akanksha Rai

C#

// C# program to find the
// incenter of a triangle
 
using System;
 
class GFG
{
 
    // Driver code
    public static void Main()
    {
        // coordinate of the vertices
        float x1 = 2, x2 = 1, x3 = 3;
        float y1 = 2, y2 = 1, y3 = 1;
        float a = 2, b = 1, c = 1;
 
        // Formula to calculate in-center
        float x
            = (a * x1 + b * x2 + c * x3) / (a + b + c);
        float y
            = (a * y1 + b * y2 + c * y3) / (a + b + c);
 
        // System.out.print(setprecision(3));
        Console.WriteLine("Incenter= "
                        + "(" + x + ", " + y + ")");
    }
}
 
// This code is contributed by vt_m.

Javascript

<script>
      // JavaScript program to find the
      // incenter of a triangle
      // Driver code
      // coordinate of the vertices
      var x1 = 2,
        x2 = 1,
        x3 = 3;
      var y1 = 2,
        y2 = 1,
        y3 = 1;
      var a = 2,
        b = 1,
        c = 1;
 
      // Formula to calculate in-center
      var x = (a * x1 + b * x2 + c * x3) / (a + b + c);
      var y = (a * y1 + b * y2 + c * y3) / (a + b + c);
 
      document.write(
        "Incenter = " + "(" + x.toFixed(1) + ", " + y.toFixed(1) + ")"
      );
    </script>

Output:

Incenter= (2.0, 1.5)

Вниманию читателя! Не прекращайте учиться сейчас. Освойте все важные концепции DSA с помощью самостоятельного курса DSA по приемлемой для студентов цене и будьте готовы к работе в отрасли. Чтобы завершить подготовку от изучения языка к DS Algo и многому другому, см. Полный курс подготовки к собеседованию .

Если вы хотите посещать живые занятия с отраслевыми экспертами, пожалуйста, обращайтесь к Geeks Classes Live и Geeks Classes Live USA.

Java

Программа для поиска центра треугольника

C++

Java

Python3

C#

Javascript

РЕКОМЕНДУЕМЫЕ СТАТЬИ