Постоянное дерево сегментов | Набор 1 (Введение)
Prerequisite : Segment Tree
Persistency in Data Structure
Дерево сегментов само по себе является отличной структурой данных, которая используется во многих случаях. В этом посте мы познакомим вас с концепцией постоянства в этой структуре данных. Постоянство просто означает сохранение изменений. Но очевидно, что сохранение изменений вызывает дополнительное потребление памяти и, следовательно, влияет на сложность времени.
Наша цель - применить постоянство в дереве сегментов, а также гарантировать, что для каждого изменения требуется не более O (log n) времени и места.
Давайте подумаем о версиях, то есть для каждого изменения в нашем дереве сегментов мы создаем его новую версию.
Мы будем рассматривать нашу первоначальную версию как версию 0. Теперь, когда мы выполняем любое обновление в дереве сегментов, мы создаем для него новую версию и аналогичным образом отслеживаем запись для всех версий.
Но создание всего дерева для каждой версии займет O (n log n) дополнительного места и O (n log n) времени. Так что на эту идею не хватает времени и памяти для большого количества версий.
Давайте воспользуемся тем фактом, что при каждом новом обновлении (скажем, обновлении точки для простоты) в дереве сегментов узлы при максимальном входе в систему будут изменяться. Итак, наша новая версия будет содержать только эти log n новых узлов, а остальные узлы будут такими же, как и в предыдущей версии. Следовательно, совершенно очевидно, что для каждой новой версии нам нужно только создать эти log n новых узлов, в то время как остальные узлы могут использоваться совместно с предыдущей версией.
Рассмотрим рисунок ниже для лучшей визуализации (щелкните изображение для лучшего просмотра): -
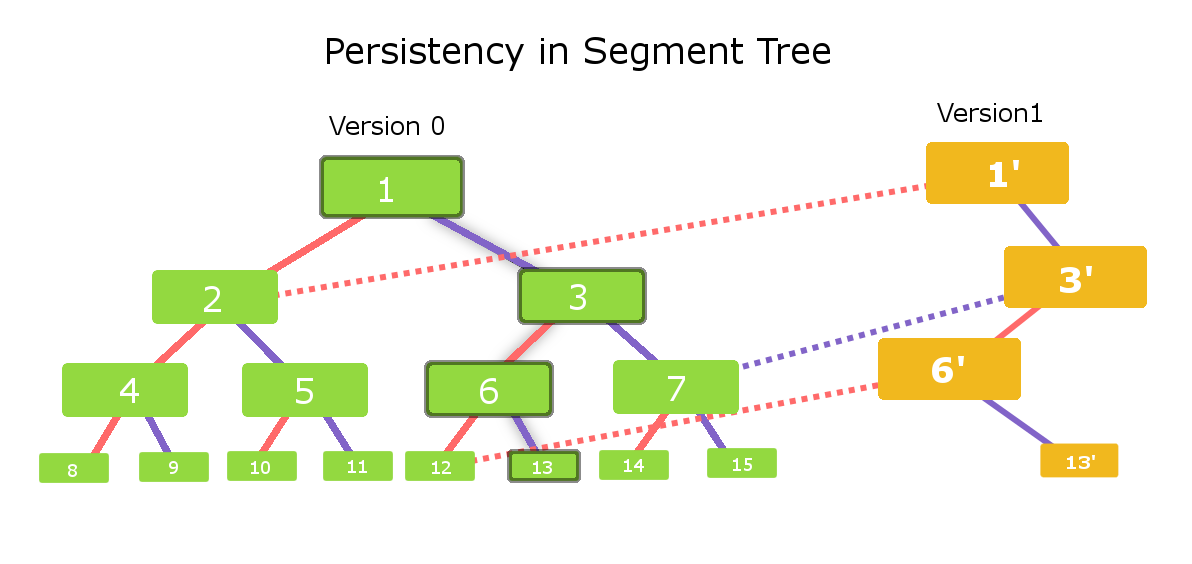
Рассмотрим сегментное дерево с зелеными узлами. Назовем это дерево сегментов версией 0 . Левый дочерний элемент каждого узла соединен сплошным красным краем, а правый дочерний элемент каждого узла соединен сплошным фиолетовым краем. Ясно, что это дерево сегментов состоит из 15 узлов.
Теперь представьте, что нам нужно внести изменения в листовой узел 13 версии 0.
Итак, затронутые узлы будут - узел 13, узел 6, узел 3, узел 1 .
Следовательно, для новой версии (Version-1) нам нужно создать только эти 4 новых узла .
Теперь давайте построим версию 1 для этого изменения в дереве сегментов. Нам нужен новый узел 1, поскольку на него влияют изменения, сделанные в узле 13. Итак, сначала мы создадим новый узел 1 ' (желтый цвет). Левый дочерний элемент для узла 1 'будет таким же, как и левый дочерний элемент для узла 1 в версии 0. Итак, мы соединяем левый дочерний узел узла 1 'с узлом 2 версии 0 (красная пунктирная линия на рисунке). Давайте теперь рассмотрим правого потомка для узла 1 'в версии 1. Нам нужно создать новый узел, поскольку он затронут. Итак, мы создаем новый узел, называемый узлом 3 ', и делаем его правильным потомком для узла 1' (сплошное пурпурное граничное соединение).
Аналогичным образом мы рассмотрим узел 3 ′ . Левый дочерний элемент затронут, поэтому мы создаем новый узел с именем node 6 ' и соединяем его сплошным красным краем с узлом 3', где правый дочерний элемент для узла 3 'будет таким же, как правый дочерний элемент узла 3 в версии- 0. Итак, мы сделаем правого дочернего элемента узла 3 в версии 0 правым дочерним элементом узла 3 ′ в версии 1 (см. Край фиолетовой черточки).
Та же процедура выполняется для узла 6 ', и мы видим, что левый дочерний элемент узла 6' будет левым дочерним элементом узла 6 в версии 0 (соединение, отмеченное красным пунктиром), а правый дочерний элемент - это вновь созданный узел, называемый узлом 13 ' (сплошной фиолетовый штриховой край).
Каждый узел желтого цвета - это вновь созданный узел, а пунктирные края - это взаимосвязь между различными версиями дерева сегментов.
Возникает вопрос: как отслеживать все версии?
- Нам нужно отслеживать только первый корневой узел для всех версий, и это будет служить цели для отслеживания всех вновь созданных узлов в разных версиях. Для этого мы можем поддерживать массив указателей на первый узел дерева сегментов для всех версий.
Давайте рассмотрим очень простую проблему, чтобы увидеть, как реализовать постоянство в дереве сегментов.
Проблема : задан массив A [] и разные операции обновления точки. каждая точечная операция для создания новой версии массива. Нам нужно ответить запросы типа Q vlr: вывести сумму элементов в диапазоне от l до r сразу после v-го обновления.
Мы создадим все версии дерева сегментов и будем отслеживать их корневой узел. Затем для каждого запроса суммы диапазона мы передадим корневой узел требуемой версии в нашу функцию запроса и выведем требуемую сумму.
Below is the implementation for the above problem:-
C++
// C++ program to implement persistent segment// tree.#include "bits/stdc++.h"using namespace std; #define MAXN 100 /* data type for individual * node in the segment tree */struct node{ // stores sum of the elements in node int val; // pointer to left and right children node* left, *right; // required constructors........ node() {} node(node* l, node* r, int v) { left = l; right = r; val = v; }}; // input arrayint arr[MAXN]; // root pointers for all versionsnode* version[MAXN]; // Constructs Version-0// Time Complexity : O(nlogn)void build(node* n,int low,int high){ if (low==high) { n->val = arr[low]; return; } int mid = (low+high) / 2; n->left = new node(NULL, NULL, 0); n->right = new node(NULL, NULL, 0); build(n->left, low, mid); build(n->right, mid+1, high); n->val = n->left->val + n->right->val;} /** * Upgrades to new Version * @param prev : points to node of previous version * @param cur : points to node of current version * Time Complexity : O(logn) * Space Complexity : O(logn) */void upgrade(node* prev, node* cur, int low, int high, int idx, int value){ if (idx > high or idx < low or low > high) return; if (low == high) { // modification in new version cur->val = value; return; } int mid = (low+high) / 2; if (idx <= mid) { // link to right child of previous version cur->right = prev->right; // create new node in current version cur->left = new node(NULL, NULL, 0); upgrade(prev->left,cur->left, low, mid, idx, value); } else { // link to left child of previous version cur->left = prev->left; // create new node for current version cur->right = new node(NULL, NULL, 0); upgrade(prev->right, cur->right, mid+1, high, idx, value); } // calculating data for current version // by combining previous version and current // modification cur->val = cur->left->val + cur->right->val;} int query(node* n, int low, int high, int l, int r){ if (l > high or r < low or low > high) return 0; if (l <= low and high <= r) return n->val; int mid = (low+high) / 2; int p1 = query(n->left,low,mid,l,r); int p2 = query(n->right,mid+1,high,l,r); return p1+p2;} int main(int argc, char const *argv[]){ int A[] = {1,2,3,4,5}; int n = sizeof(A)/sizeof(int); for (int i=0; i<n; i++) arr[i] = A[i]; // creating Version-0 node* root = new node(NULL, NULL, 0); build(root, 0, n-1); // storing root node for version-0 version[0] = root; // upgrading to version-1 version[1] = new node(NULL, NULL, 0); upgrade(version[0], version[1], 0, n-1, 4, 1); // upgrading to version-2 version[2] = new node(NULL, NULL, 0); upgrade(version[1],version[2], 0, n-1, 2, 10); cout << "In version 1 , query(0,4) : "; cout << query(version[1], 0, n-1, 0, 4) << endl; cout << "In version 2 , query(3,4) : "; cout << query(version[2], 0, n-1, 3, 4) << endl; cout << "In version 0 , query(0,3) : "; cout << query(version[0], 0, n-1, 0, 3) << endl; return 0;} |
Java
// Java program to implement persistent// segment tree.class GFG{ // Declaring maximum numberstatic Integer MAXN = 100; // Making Node for treestatic class node { // Stores sum of the elements in node int val; // Reference to left and right children node left, right; // Required constructors.. node() {} // Node constructor for l,r,v node(node l, node r, int v) { left = l; right = r; val = v; }} // Input arraystatic int[] arr = new int[MAXN]; // Root pointers for all versionsstatic node version[] = new node[MAXN]; // Constructs Version-0// Time Complexity : O(nlogn)static void build(node n, int low, int high){ if (low == high) { n.val = arr[low]; return; } int mid = (low + high) / 2; n.left = new node(null, null, 0); n.right = new node(null, null, 0); build(n.left, low, mid); build(n.right, mid + 1, high); n.val = n.left.val + n.right.val;} /* Upgrades to new Version * @param prev : points to node of previous version * @param cur : points to node of current version * Time Complexity : O(logn) * Space Complexity : O(logn) */static void upgrade(node prev, node cur, int low, int high, int idx, int value){ if (idx > high || idx < low || low > high) return; if (low == high) { // Modification in new version cur.val = value; return; } int mid = (low + high) / 2; if (idx <= mid) { // Link to right child of previous version cur.right = prev.right; // Create new node in current version cur.left = new node(null, null, 0); upgrade(prev.left, cur.left, low, mid, idx, value); } else { // Link to left child of previous version cur.left = prev.left; // Create new node for current version cur.right = new node(null, null, 0); upgrade(prev.right, cur.right, mid + 1, high, idx, value); } // Calculating data for current version // by combining previous version and current // modification cur.val = cur.left.val + cur.right.val;} static int query(node n, int low, int high, int l, int r){ if (l > high || r < low || low > high) return 0; if (l <= low && high <= r) return n.val; int mid = (low + high) / 2; int p1 = query(n.left, low, mid, l, r); int p2 = query(n.right, mid + 1, high, l, r); return p1 + p2;} // Driver codepublic static void main(String[] args){ int A[] = { 1, 2, 3, 4, 5 }; int n = A.length; for(int i = 0; i < n; i++) arr[i] = A[i]; // Creating Version-0 node root = new node(null, null, 0); build(root, 0, n - 1); // Storing root node for version-0 version[0] = root; // Upgrading to version-1 version[1] = new node(null, null, 0); upgrade(version[0], version[1], 0, n - 1, 4, 1); // Upgrading to version-2 version[2] = new node(null, null, 0); upgrade(version[1], version[2], 0, n - 1, 2, 10); // For print System.out.print("In version 1 , query(0,4) : "); System.out.print(query(version[1], 0, n - 1, 0, 4)); System.out.print("
In version 2 , query(3,4) : "); System.out.print(query(version[2], 0, n - 1, 3, 4)); System.out.print("
In version 0 , query(0,3) : "); System.out.print(query(version[0], 0, n - 1, 0, 3));}} // This code is contributed by mark_85 |
C#
// C# program to implement persistent// segment tree.using System; class node{ // Stores sum of the elements in node public int val; // Reference to left and right children public node left, right; // Required constructors.. public node() {} // Node constructor for l,r,v public node(node l, node r, int v) { left = l; right = r; val = v; }} class GFG{ // Declaring maximum numberstatic int MAXN = 100; // Making Node for tree// Input arraystatic int[] arr = new int[MAXN]; // Root pointers for all versionsstatic node[] version = new node[MAXN]; // Constructs Version-0// Time Complexity : O(nlogn)static void build(node n, int low, int high){ if (low == high) { n.val = arr[low]; РЕКОМЕНДУЕМЫЕ СТАТЬИ |