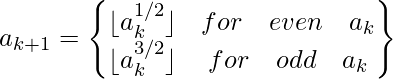Последовательность жонглера | Набор 2 (с использованием рекурсии)
Последовательность жонглера — это последовательность целых чисел, в которой первый член начинается с положительного целого числа a, а остальные члены генерируются из непосредственно предыдущего члена с использованием приведенного ниже рекуррентного соотношения:
Juggler Sequence starting with number 3:
5, 11, 36, 6, 2, 1
Juggler Sequence starting with number 9:
9, 27, 140, 11, 36, 6, 2, 1
Учитывая число N , мы должны напечатать последовательность жонглера для этого числа в качестве первого члена последовательности.
Примеры :
Input: N = 9
Output: 9, 27, 140, 11, 36, 6, 2, 1
We start with 9 and use above formula to get next terms.Input: N = 6
Output: 6, 2, 1
Итеративный подход: мы уже видели итеративный подход в наборе 1 этой задачи.
Рекурсивный подход: в этом подходе мы будем рекурсивно проходить, начиная с N. Выполните следующие шаги для каждого рекурсивного шага.
- Выведите значение N
- Если N достигло 1 , конец рекурсии
- В противном случае следуйте формуле, основанной на нечетном или четном числе, и вызовите рекурсивную функцию для вновь полученного числа.
Ниже представлена реализация подхода:
Временная сложность: O(N)
Вспомогательное пространство: O(1)