Оптимальное двоичное дерево поиска | ДП-24
Дан отсортированный ключ массива [0 .. n-1] ключей поиска и массив freq [0 .. n-1] счетчиков частоты, где freq [i] - количество поисков ключей [i] . Постройте двоичное дерево поиска по всем ключам так, чтобы общая стоимость всех поисков была как можно меньше.
Давайте сначала определим стоимость BST. Стоимость узла BST - это уровень этого узла, умноженный на его частоту. Уровень корня - 1.
Примеры:
Ввод: keys [] = {10, 12}, freq [] = {34, 50}
Могут быть следующие два возможных BST
10 12
/
12 10
I II
Частота поисков 10 и 12 - 34 и 50 соответственно.
Стоимость дерева I составляет 34 * 1 + 50 * 2 = 134.
Стоимость дерева II составляет 50 * 1 + 34 * 2 = 118.
Ввод: keys [] = {10, 12, 20}, freq [] = {34, 8, 50}
Возможны следующие BST
10 12 20 10 20
/ / /
12 10 20 12 20 10
/ /
20 10 12 12
I II III IV V
Среди всех возможных BST стоимость пятого BST минимальна.
Стоимость пятого BST составляет 1 * 50 + 2 * 34 + 3 * 8 = 142.1) Optimal Substructure:
The optimal cost for freq[i..j] can be recursively calculated using the following formula. 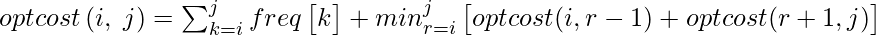
We need to calculate optCost(0, n-1) to find the result.
The idea of above formula is simple, we one by one try all nodes as root (r varies from i to j in second term). When we make rth node as root, we recursively calculate optimal cost from i to r-1 and r+1 to j.
We add sum of frequencies from i to j (see first term in the above formula), this is added because every search will go through root and one comparison will be done for every search.
2) Overlapping Subproblems
Following is recursive implementation that simply follows the recursive structure mentioned above.
C++
// A naive recursive implementation of// optimal binary search tree problem#include <bits/stdc++.h>using namespace std;// A utility function to get sum of// array elements freq[i] to freq[j]int sum(int freq[], int i, int j);// A recursive function to calculate// cost of optimal binary search treeint optCost(int freq[], int i, int j){ // Base cases if (j < i) // no elements in this subarray return 0; if (j == i) // one element in this subarray return freq[i]; // Get sum of freq[i], freq[i+1], ... freq[j] int fsum = sum(freq, i, j); // Initialize minimum value int min = INT_MAX; // One by one consider all elements // as root and recursively find cost // of the BST, compare the cost with // min and update min if needed for (int r = i; r <= j; ++r) { int cost = optCost(freq, i, r - 1) + optCost(freq, r + 1, j); if (cost < min) min = cost; } // Return minimum value return min + fsum;}// The main function that calculates// minimum cost of a Binary Search Tree.// It mainly uses optCost() to find// the optimal cost.int optimalSearchTree(int keys[], int freq[], int n){ // Here array keys[] is assumed to be // sorted in increasing order. If keys[] // is not sorted, then add code to sort // keys, and rearrange freq[] accordingly. return optCost(freq, 0, n - 1);}// A utility function to get sum of// array elements freq[i] to freq[j]int sum(int freq[], int i, int j){ int s = 0; for (int k = i; k <= j; k++) s += freq[k]; return s;}// Driver Codeint main(){ int keys[] = {10, 12, 20}; int freq[] = {34, 8, 50}; int n = sizeof(keys) / sizeof(keys[0]); cout << "Cost of Optimal BST is " << optimalSearchTree(keys, freq, n); return 0;}// This is code is contributed// by rathbhupendra |
C
// A naive recursive implementation of optimal binary// search tree problem#include <stdio.h>#include <limits.h>// A utility function to get sum of array elements// freq[i] to freq[j]int sum(int freq[], int i, int j);// A recursive function to calculate cost of optimal// binary search treeint optCost(int freq[], int i, int j){ // Base cases if (j < i) // no elements in this subarray return 0; if (j == i) // one element in this subarray return freq[i]; // Get sum of freq[i], freq[i+1], ... freq[j] int fsum = sum(freq, i, j); // Initialize minimum value int min = INT_MAX; // One by one consider all elements as root and // recursively find cost of the BST, compare the // cost with min and update min if needed for (int r = i; r <= j; ++r) { int cost = optCost(freq, i, r-1) + optCost(freq, r+1, j); if (cost < min) min = cost; } // Return minimum value return min + fsum;}// The main function that calculates minimum cost of// a Binary Search Tree. It mainly uses optCost() to// find the optimal cost.int optimalSearchTree(int keys[], int freq[], int n){ // Here array keys[] is assumed to be sorted in // increasing order. If keys[] is not sorted, then // add code to sort keys, and rearrange freq[] // accordingly. return optCost(freq, 0, n-1);}// A utility function to get sum of array elements// freq[i] to freq[j]int sum(int freq[], int i, int j){ int s = 0; for (int k = i; k <=j; k++) s += freq[k]; return s;}// Driver program to test above functionsint main(){ int keys[] = {10, 12, 20}; int freq[] = {34, 8, 50}; int n = sizeof(keys)/sizeof(keys[0]); printf("Cost of Optimal BST is %d ", optimalSearchTree(keys, freq, n)); return 0;} |
Java
// A naive recursive implementation of optimal binary// search tree problempublic class GFG{ // A recursive function to calculate cost of // optimal binary search tree static int optCost(int freq[], int i, int j) { // Base cases if (j < i) // no elements in this subarray return 0; if (j == i) // one element in this subarray return freq[i]; // Get sum of freq[i], freq[i+1], ... freq[j] int fsum = sum(freq, i, j); // Initialize minimum value int min = Integer.MAX_VALUE; // One by one consider all elements as root and // recursively find cost of the BST, compare the // cost with min and update min if needed for (int r = i; r <= j; ++r) { int cost = optCost(freq, i, r-1) + optCost(freq, r+1, j); if (cost < min) min = cost; } // Return minimum value return min + fsum; } // The main function that calculates minimum cost of // a Binary Search Tree. It mainly uses optCost() to // find the optimal cost. static int optimalSearchTree(int keys[], int freq[], int n) { // Here array keys[] is assumed to be sorted in // increasing order. If keys[] is not sorted, then // add code to sort keys, and rearrange freq[] // accordingly. return optCost(freq, 0, n-1); } // A utility function to get sum of array elements // freq[i] to freq[j] static int sum(int freq[], int i, int j) { int s = 0; for (int k = i; k <=j; k++) s += freq[k]; return s; } // Driver code public static void main(String[] args) { int keys[] = {10, 12, 20}; int freq[] = {34, 8, 50}; int n = keys.length; System.out.println("Cost of Optimal BST is " + optimalSearchTree(keys, freq, n)); }}// This code is contributed by Sumit Ghosh |
Python3
# A naive recursive implementation of# optimal binary search tree problem# A recursive function to calculate# cost of optimal binary search treedef optCost(freq, i, j): # Base cases if j < i: # no elements in this subarray return 0 if j == i: # one element in this subarray return freq[i] # Get sum of freq[i], freq[i+1], ... freq[j] fsum = Sum(freq, i, j) # Initialize minimum value Min = 999999999999 # One by one consider all elements as # root and recursively find cost of # the BST, compare the cost with min # and update min if needed for r in range(i, j + 1): cost = (optCost(freq, i, r - 1) + optCost(freq, r + 1, j)) if cost < Min: Min = cost # Return minimum value return Min + fsum# The main function that calculates minimum# cost of a Binary Search Tree. It mainly# uses optCost() to find the optimal cost.def optimalSearchTree(keys, freq, n): # Here array keys[] is assumed to be # sorted in increasing order. If keys[] # is not sorted, then add code to sort # keys, and rearrange freq[] accordingly. return optCost(freq, 0, n - 1)# A utility function to get sum of# array elements freq[i] to freq[j]def Sum(freq, i, j): s = 0 for k in range(i, j + 1): s += freq[k] return s# Driver Codeif __name__ == "__main__": keys = [10, 12, 20] freq = [34, 8, 50] n = len(keys) print("Cost of Optimal BST is", optimalSearchTree(keys, freq, n)) # This code is contributed by PranchalK |
C#
// A naive recursive implementation of optimal binary// search tree problemusing System;class GFG{ // A recursive function to calculate cost of // optimal binary search tree static int optCost(int []freq, int i, int j) { // Base cases // no elements in this subarray if (j < i) return 0; // one element in this subarray if (j == i) return freq[i]; // Get sum of freq[i], freq[i+1], ... freq[j] int fsum = sum(freq, i, j); // Initialize minimum value int min = int.MaxValue; // One by one consider all elements as root and // recursively find cost of the BST, compare the // cost with min and update min if needed for (int r = i; r <= j; ++r) { int cost = optCost(freq, i, r-1) + optCost(freq, r+1, j); if (cost < min) min = cost; } // Return minimum value return min + fsum; } // The main function that calculates minimum cost of // a Binary Search Tree. It mainly uses optCost() to // find the optimal cost. static int optimalSearchTree(int []keys, int []freq, int n) { // Here array keys[] is assumed to be sorted in // increasing order. If keys[] is not sorted, then // add code to sort keys, and rearrange freq[] // accordingly. return optCost(freq, 0, n-1); } // A utility function to get sum of array elements // freq[i] to freq[j] static int sum(int []freq, int i, int j) { int s = 0; for (int k = i; k <=j; k++) s += freq[k]; return s; } // Driver code public static void Main() { int []keys = {10, 12, 20}; int []freq = {34, 8, 50}; int n = keys.Length; Console.Write("Cost of Optimal BST is " + optimalSearchTree(keys, freq, n)); }}// This code is contributed by Sam007 |
Javascript
<script>//Javascript Implementation // A recursive function to calculate// cost of optimal binary search treefunction optCost(freq, i, j){ // Base cases if (j < i) // no elements in this subarray &nb
РЕКОМЕНДУЕМЫЕ СТАТЬИ |