Определите, содержат ли только две параллельные прямые все точки координат или нет

Опубликовано: 14 Января, 2022

Дан массив, который представляет координаты y набора точек на координатной плоскости, где (i, arr [i]) представляет одну точку. Найдите, можно ли нарисовать пару параллельных линий, которые включают все заданные координатные точки, а также обе линии должны содержать точку. Выведите 1, если возможно, и 0, если невозможно.

Примеры:

Input: arr[] = {1, 4, 3, 6, 5}; 
Output: 1 
(1, 1), (3, 3) and (5, 5) lie on one line 
where as (2, 4) and (4, 6) lie on another line.
Input: arr[] = {2, 4, 3, 6, 5}; 
Output: 0 
Minimum 3 lines needed to cover all points. 

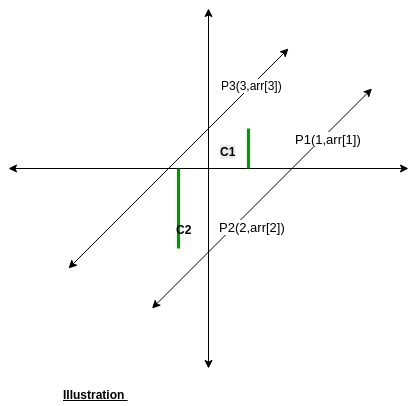
Рекомендуется: сначала попробуйте свой подход в {IDE}, прежде чем переходить к решению.

Подход: наклон линии, образованной точками (x1, y1) и (x2, y2), равен y2-y2 / x2-x1. Поскольку данный массив состоит из координат точек как (i, arr [i]). Итак, (arr [2] -arr [1]) / (2-1) - это наклон линии, образованной (1, arr [i]) и (2, arr [2]). Примите во внимание только три точки, например, P0 (0, arr [0]), P1 (1, arr [1]) и P2 (2, arr [2]), поскольку требуется только две параллельные линии, это обязательно что две из этих трех точек лежат на одной линии. Итак, возможны три случая:

  • P0 и P1 находятся на одной прямой, поэтому их наклон будет arr [1] -arr [0]
  • P1 и P2 находятся на одной прямой, поэтому их наклон будет arr [2] -arr [1]
  • P0 и P2 находятся на одной прямой, поэтому их наклон будет arr [2] -arr [0] / 2

Возьмем один из трех случаев, скажем, P0 и P1 лежат на одной прямой, в этом случае пусть m = arr [1] -arr [0] - наш наклон. Для общей точки в массиве (i, arr [i]) уравнение прямой выглядит следующим образом:

=> (y-y1) = m (x-x1)
=> y-arr[i] = m (x-i)
=> y-mx = arr[i] - mi

Теперь, поскольку y-mx = c является общим уравнением прямой, здесь c = arr [i] -mi. Теперь, если решение будет возможным для данного массива, тогда у нас должно быть ровно два перехвата (c).
Итак, если существуют два различных перехвата для любого из трех возможных вышеупомянутых, требуемое решение возможно и выведите 1 иначе 0.

Below is the implementation of the above approach:  

C++

// C++ implementation of the above approach
#include <bits/stdc++.h>
using namespace std;
 
// Find if slope is good with only two intercept
bool isSlopeGood(double slope, int arr[], int n)
{
    set<double> setOfLines;
    for (int i = 0; i < n; i++)
        setOfLines.insert(arr[i] - slope * (i));
 
    // if set of lines have only two distinct intercept
    return setOfLines.size() == 2;
}
 
// Function to check if required solution exist
bool checkForParallel(int arr[], int n)
{
    // check the result by processing
    // the slope by starting three points
    bool slope1 = isSlopeGood(arr[1] - arr[0], arr, n);
    bool slope2 = isSlopeGood(arr[2] - arr[1], arr, n);
    bool slope3 = isSlopeGood((arr[2] - arr[0]) / 2, arr, n);
 
    return (slope1 || slope2 || slope3);
}
 
// Driver code
int main()
{
    int arr[] = { 1, 6, 3, 8, 5 };
    int n = sizeof(arr) / sizeof(arr[0]);
    cout << (int)checkForParallel(arr, n);
 
    return 0;
}

Java

// Java implementation of the above approach
import java.util.*;
 
class GfG
{
 
// Find if slope is good
// with only two intercept
static boolean isSlopeGood(double slope,
                        int arr[], int n)
{
    Set<Double> setOfLines = new HashSet<Double> ();
    for (int i = 0; i < n; i++)
        setOfLines.add(arr[i] - slope * (i));
 
    // if set of lines have only two distinct intercept
    return setOfLines.size() == 2;
}
 
// Function to check if required solution exist
static boolean checkForParallel(int arr[], int n)
{
    // check the result by processing
    // the slope by starting three points
    boolean slope1 = isSlopeGood(arr[1] - arr[0], arr, n);
    boolean slope2 = isSlopeGood(arr[2] - arr[1], arr, n);
    boolean slope3 = isSlopeGood((arr[2] - arr[0]) / 2, arr, n);
 
    return (slope1 == true || slope2 == true || slope3 == true);
}
 
// Driver code
public static void main(String[] args)
{
    int arr[] = { 1, 6, 3, 8, 5 };
    int n = arr.length;
    if(checkForParallel(arr, n) == true)
    System.out.println("1");
    else
    System.out.println("0");
}
}
 
// This code is contributed by Prerna Saini.

Python3

# Python3 implementation of the
# above approach
 
# Find if slope is good with only
# two intercept
def isSlopeGood(slope, arr, n):
 
    setOfLines = dict()
    for i in range(n):
        setOfLines[arr[i] - slope * (i)] = 1
 
    # if set of lines have only
    # two distinct intercept
    return len(setOfLines) == 2
 
# Function to check if required solution exist
def checkForParallel(arr, n):
     
    # check the result by processing
    # the slope by starting three points
    slope1 = isSlopeGood(arr[1] - arr[0], arr, n)
    slope2 = isSlopeGood(arr[2] - arr[1], arr, n)
    slope3 = isSlopeGood((arr[2] - arr[0]) // 2, arr, n)
 
    return (slope1 or slope2 or slope3)
 
# Driver code
arr = [1, 6, 3, 8, 5 ]
n = len(arr)
if checkForParallel(arr, n):
    print(1)
else:
    print(0)
     
# This code is contributed by Mohit Kumar   

C#

// C# implementation of the above approach
using System;
using System.Collections.Generic;
 
class GfG
{
 
// Find if slope is good
// with only two intercept
static bool isSlopeGood(double slope,
                        int []arr, int n)
{
 
    HashSet<Double> setOfLines = new HashSet<Double> ();
    for (int i = 0; i < n; i++)
        setOfLines.Add(arr[i] - slope * (i));
 
    // if set of lines have only two distinct intercept
    return setOfLines.Count == 2;
}
 
// Function to check if required solution exist
static bool checkForParallel(int []arr, int n)
{
    // check the result by processing
    // the slope by starting three points
    bool slope1 = isSlopeGood(arr[1] - arr[0], arr, n);
    bool slope2 = isSlopeGood(arr[2] - arr[1], arr, n);
    bool slope3 = isSlopeGood((arr[2] - arr[0]) / 2, arr, n);
 
    return (slope1 == true || slope2 == true || slope3 == true);
}
 
// Driver code
public static void Main()
{
    int []arr = { 1, 6, 3, 8, 5 };
    int n = arr.Length;
    if(checkForParallel(arr, n) == true)
        Console.WriteLine("1");
    else
        Console.WriteLine("0");
}
}
 
// This code is contributed by Ryuga.

PHP

<?php
// PHP implementation of the above approach
 
// Find if slope is good with only
// two intercept
function isSlopeGood($slope, $arr, $n)
{
    $setOfLines = array_fill(0, max($arr) * $n, 0);
    for ($i = 0; $i < $n; $i++)
        $setOfLines[$arr[$i] - $slope * $i] = 1;
    $setOfLines = array_unique($setOfLines);
     
    // if set of lines have only two
    // distinct intercept
    return (count($setOfLines) == 2);
}
 
// Function to check if required
// solution exist
function checkForParallel($arr, $n)
{
    // check the result by processing
    // the slope by starting three points
    $slope1 = isSlopeGood($arr[1] - $arr[0],
                                    $arr, $n);
    $slope2 = isSlopeGood($arr[2] - $arr[1],
                                    $arr, $n);
    $slope3 = isSlopeGood((int)(($arr[2] -
                                 $arr[0]) / 2),
                                 $arr, $n);
 
    return ($slope1 || $slope2 || $slope3);
}
 
// Driver code
$arr = array( 1, 6, 3, 8, 5 );
$n = count($arr);
echo (int)checkForParallel($arr, $n) . " ";
 
// This code is contributed by mits
?>

Javascript

<script>
 
// Javascript implementation of the above approach
 
// Find if slope is good with only two intercept
function isSlopeGood(slope, arr, n)
{
    var setOfLines = new Set();
    for (var i = 0; i < n; i++)
        setOfLines.add(arr[i] - slope * (i));
 
    // if set of lines have only two distinct intercept
    return setOfLines.size == 2;
}
 
// Function to check if required solution exist
function checkForParallel(arr, n)
{
    // check the result by processing
    // the slope by starting three points
    var slope1 = isSlopeGood(arr[1] - arr[0], arr, n);
    var slope2 = isSlopeGood(arr[2] - arr[1], arr, n);
    var slope3 = isSlopeGood(parseInt((arr[2] - arr[0]) / 2), arr, n);
 
    if(slope1 || slope2 || slope3)
    {
        return 1;
    }
    return 0;
}
 
// Driver code
var arr = [ 1, 6, 3, 8, 5 ];
var n = arr.length;
document.write( checkForParallel(arr, n));
 
</script>
Output: 
1

 

Вниманию читателя! Не прекращайте учиться сейчас. Освойте все важные концепции DSA с помощью самостоятельного курса DSA по приемлемой для студентов цене и будьте готовы к работе в отрасли. Чтобы завершить подготовку от изучения языка к DS Algo и многому другому, см. Полный курс подготовки к собеседованию .

Если вы хотите посещать живые занятия с отраслевыми экспертами, пожалуйста, обращайтесь к Geeks Classes Live и Geeks Classes Live USA.

РЕКОМЕНДУЕМЫЕ СТАТЬИ