Объем тела вращения
Тело вращения создается путем вращения плоской области R вокруг линии L, известной как ось вращения на плоскости. На изображении ниже показан пример твердого тела вращения.
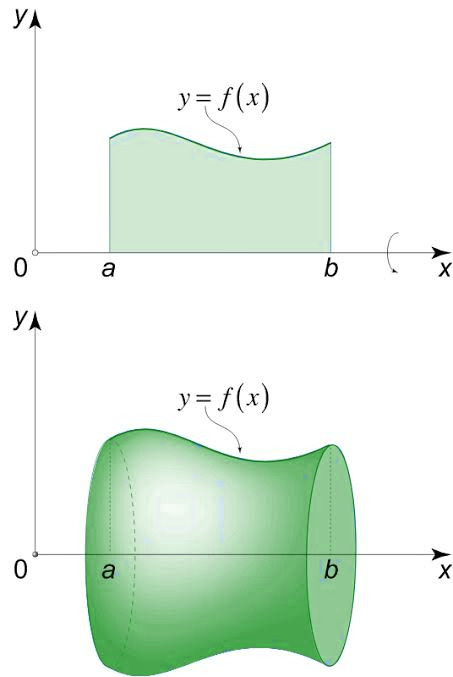
Мы будем вычислять объем тела вращения, когда уравнение кривой задано в параметрической форме и полярной форме.
- Параметрическая форма:
Если уравнение кривой в параметрической форме имеет вид:х = f (t) и y = g (t)
Если t изменяется от t 1 до t 2 , то объем вращения:
- О оси x -
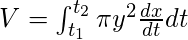
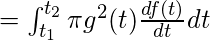
- О оси Y -
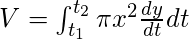
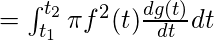
- О оси x -
- Полярная форма:
Учитывая уравнение кривой в полярной форме как r = f (θ), где θ изменяется от θ 1 до θ 2 , объем вращения рассчитывается по приведенным формулам:- Относительно начальной линии OX, т. Е. Оси x (θ = 0) -
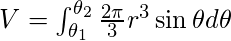
- О прямой, перпендикулярной исходной, т.е. вдоль OY (θ = π / 2) -
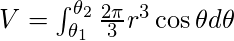
- Относительно начальной линии OX, т. Е. Оси x (θ = 0) -
Посмотрим на следующие примеры.
Пример-1:
Определите объем тела вращения, образованный вращением кривой, параметрические уравнения которой:
Х = 2t + 3 и у = 4t 2 -9
О оси X для t = от -3/2 до 3/2.
Объяснение :
Мы знаем, что объем твердого тела, вращающийся вокруг оси x, когда уравнение имеет параметрическую форму, определяется выражением 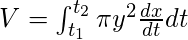
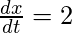
Используя это значение, мы получаем 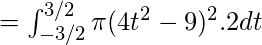
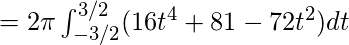
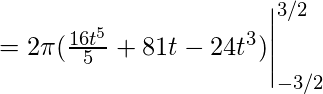
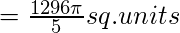
Пример-2:
Найдите объем твердого тела, образованный вращающейся кривой r = 2a cos θ вокруг начальной линии OX.
Объяснение :
Мы знаем, что объем твердого тела, образующийся при вращении вокруг OX, когда уравнение находится в полярной форме, определяется выражением 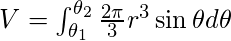
Также для OX θ = 0
Так 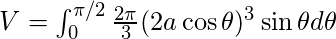
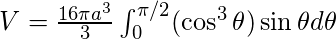
Положил 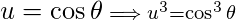
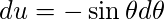
Используя эти значения, получаем 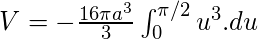
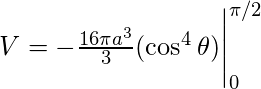
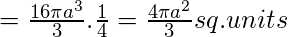
Вниманию читателя! Не переставай учиться сейчас. Ознакомьтесь со всеми важными концепциями теории CS для собеседований по SDE с помощью курса теории CS по доступной для студентов цене и будьте готовы к работе в отрасли.