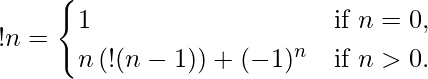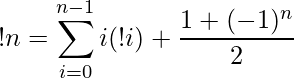Найти субфакториал числа
По заданному целому N задача состоит в том, чтобы найти субфакториал числа, представленного как !N. Субфакториал числа определяется с использованием приведенного ниже рекуррентного отношения числа N :
!N = (N-1) [ !(N-2) + !(N-1) ]
where !1 = 0 and !0 = 1
Некоторые из субфакториалов:
| н | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ! н | 1 | 0 | 1 | 2 | 9 | 44 | 265 | 1 854 | 14 833 | 133, 496 | 1 334 961 | 14, 684, 570 | 176, 214, 841 | 2, 290, 792, 932 |
Примеры:
Input: N = 4
Output: 9
Explanation:
!4 = !(4-1)*4 + (-1)4 = !3*4 + 1
!3 = !(3 – 1)*3 + (-1)3 = !2*3 – 1
!2 = !(2 – 1)*2 + (-1)2 = !1*2 + 1
!1 = !(1 – 1)*1 + (-1)1 = !0*1 – 1
Since !0 = 1, therefore !1 = 0, !2 = 1, !3 = 2 and !4 = 9.Input: N = 0
Output: 1
Подход: субфакториал числа N также можно рассчитать как:
Expanding this gives
=> !N = ( N! )*( 1 – 1/(1!) + (1/2!) – (1/3!) …….. (1/N!)*(-1)N )
Следовательно, приведенный выше ряд можно использовать для нахождения субфакториала числа N. Выполните следующие шаги, чтобы узнать, как это сделать:
- Инициализируйте переменные, скажем, res = 0 , fact = 1 и count = 0 .
- Переберите диапазон от 1 до N, используя i , и сделайте следующее:
- Обновить факт как факт*i.
- Если счет четный , обновите res как res = res – (1/fact) .
- Если количество нечетное , обновите res как res = res + (1/fact) .
- Увеличьте значение счетчика на 1.
- Наконец, верните fact*(1 + res) .
Ниже приведена реализация вышеуказанного подхода:
Временная сложность: O(N)
Вспомогательное пространство: O(1)