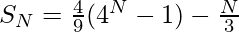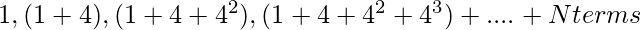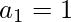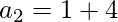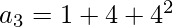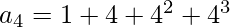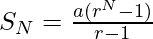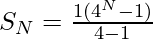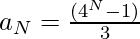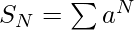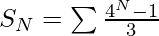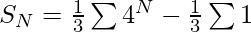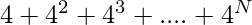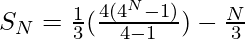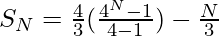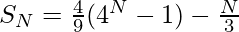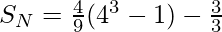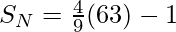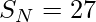Найдите сумму N членов ряда 1, (1+4), (1+4+4^2), (1+4+4^2+4^3), …..

Учитывая положительное целое число, N . Найдите сумму первых N членов ряда:

1, (1+4), (1+4+4²), (1+4+4²+4³), …., till N terms

Примеры:

Input: N = 3
Output: 27

Input: N = 5
Output: 453

Подход:

1st term = 1

2nd term = (1 + 4)

3rd term = (1 + 4 + 4 ^ 2)

4th term = (1 + 4 + 4 ^ 2 + 4 ^ 3)

.

.

Nth term = (1 + 4 + 4 ^ 2+….+ 4 ^ (N – 2) + 4 ^(N – 1))

Последовательность формируется с использованием следующего шаблона. Для любого значения N-

Вывод:

Следующая серия шагов может быть использована для вывода формулы для нахождения суммы N терминов:

The series 

can be decomposed as-

                               -(1)

The equation (1) is in G.P. with

First term a = 1

Common ration r = 4

The sum of N terms in G.P. for r>1 is

Substituting the values of a and r in the above equation, we get-

Thus, the term

The sum of the series 1, (1+4), (1+4+4^{2}), (1+4+4^{2}+4^{3})+….+N terms can be represented as-

      -(2)

The equation-

is in G.P. with 

First term a = 4

Common ratio r = 4

Applying the formula of sum of G.P.-

                                               -(3)

Substituting equation (3) in equation (2), we get-

Иллюстрация:

Input: N = 3
Output: 11
Explanation:

Ниже приведена реализация вышеуказанного подхода:

Временная сложность: O(1)
Вспомогательное пространство: O(1)