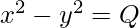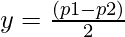Найдите два целых числа X и Y с заданными НОД P и заданной разницей между их квадратами Q.
Даны два целых числа P и Q , задача состоит в том, чтобы найти любые два целых числа, у которых наибольший общий делитель (НОД) равен P , а разница между их квадратами равна Q. Если таких целых чисел не существует, выведите «-1» .
Примеры:
Input: P = 3, Q = 27
Output: 6 3
Explanation:
Consider the two number as 6, 3. Now, the GCD(6, 3) = 3 and 6*6 – 3*3 = 27 which satisfies the condition.Input: P = 1, Q = 100
Output: -1
Подход: Данная задача может быть решена с использованием следующих наблюдений:
Данное уравнение также можно записать в виде:
=>
=>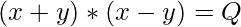
Теперь для интегрального решения данного уравнения:
(x+y)(x-y) is always an integer
=> (x+y)(x-y) are divisors of Q
Пусть (x + y) = p1 и (x + y) = p2
— два уравнения, где p1 и p2 — делители Q
такое, что p1 * p2 = Q .
Решая два приведенных выше уравнения, мы имеем:
=>
and
Из приведенных выше расчетов, чтобы x и y были целыми, сумма делителей должна быть четной . Поскольку существует 4 возможных значения для двух значений x и y как (+x, +y), (+x, -y), (-x, +y) и (-x, -y) .
Следовательно, общее количество возможных решений равно 4*(количество пар делителей с четной суммой) .
Теперь среди этих пар найдите пару с НОД в виде P и выведите эту пару. Если такой пары не существует, выведите -1.
Ниже приведена реализация вышеуказанного подхода:
Временная сложность: O(sqrt(Q))
Вспомогательное пространство: O(1)