Минимальный путь суммы в трехмерном массиве
Опубликовано: 20 Января, 2022
Для трехмерного массива arr [l] [m] [n] задача состоит в том, чтобы найти минимальную сумму путей от первой ячейки массива до последней ячейки массива. Мы можем перейти только к соседнему элементу, то есть из данной ячейки (i, j, k), ячеек (i + 1, j, k), (i, j + 1, k) и (i, j, k + 1) можно обойти, диагональный обход не допускается. Мы можем считать, что все затраты являются положительными целыми числами.
Примеры:
Ввод: arr [] [] [] = {{{1, 2}, {3, 4}},
{{4, 8}, {5, 2}}};
Выход: 9
Пояснение: arr [0] [0] [0] + arr [0] [0] [1] +
arr [0] [1] [1] + arr [1] [1] [1]
Ввод: {{{1, 2}, {4, 3}},
{{3, 4}, {2, 1}}};
Выход: 7
Пояснение: arr [0] [0] [0] + arr [0] [0] [1] +
arr [0] [1] [1] + arr [1] [1] [1]
Рекомендуется: сначала попробуйте свой подход в {IDE}, прежде чем переходить к решению.
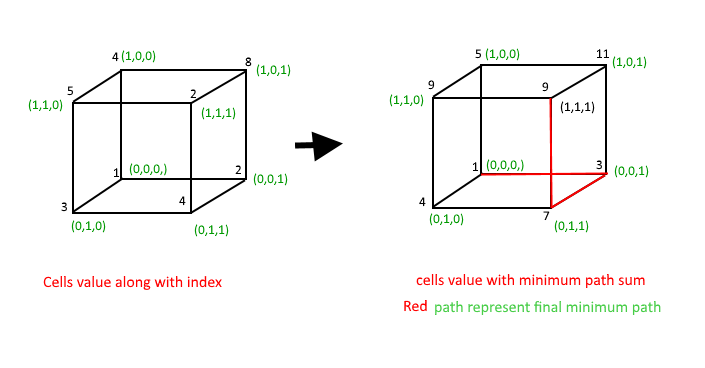
Давайте рассмотрим трехмерный массив arr [2] [2] [2], представленный кубоидом, имеющим следующие значения:
arr [] [] [] = {{{1, 2}, {3, 4}},
{{4, 8}, {5, 2}}};
Результат = 9 рассчитывается как:
Эта проблема аналогична минимальной стоимости пути. и может быть решена с помощью динамического программирования /
// Массив для хранения результата
int tSum [l] [m] [n];
tSum [0] [0] [0] = arr [0] [0] [0];
/ * Инициализируем первую строку массива tSum * /
для (i = 1; i <l; i ++)
tSum [i] [0] [0] = tSum [i-1] [0] [0] + arr [i] [0] [0];
/ * Инициализируем первый столбец массива tSum * /
для (j = 1; j <m; j ++)
tSum [0] [j] [0] = tSum [0] [j-1] [0] + arr [0] [j] [0];
/ * Инициализируем первую ширину массива tSum * /
для (k = 1; k <n; k ++)
tSum [0] [0] [k] = tSum [0] [0] [k-1] + arr [0] [0] [k];
/ * Инициализируем первую строку - Первый столбец tSum
множество */
для (i = 1; i <l; i ++)
для (j = 1; j <m; j ++)
tSum [i] [j] [0] = min (tSum [i-1] [j] [0],
tSum [i] [j-1] [0],
INT_MAX)
+ arr [i] [j] [0];
/ * Инициализируем первую строку - Первая ширина tSum
множество */
для (i = 1; i <l; i ++)
для (k = 1; k <n; k ++)
tSum [i] [0] [k] = min (tSum [i-1] [0] [k],
tSum [i] [0] [k-1],
INT_MAX)
+ arr [i] [0] [k];
/ * Инициализируем первую ширину - Первый столбец
tSum массив * /
для (k = 1; k <n; k ++)
для (j = 1; j <m; j ++)
tSum [0] [j] [k] = min (tSum [0] [j] [k-1],
tSum [0] [j-1] [k],
INT_MAX)
+ arr [0] [j] [k];
/ * Строим остальную часть массива tSum * /
для (i = 1; i <l; i ++)
для (j = 1; j <m; j ++)
для (k = 1; k <n; k ++)
tSum [i] [j] [k] = min (tSum [i-1] [j] [k],
tSum [i] [j-1] [k],
tSum [i] [j] [k-1])
+ arr [i] [j] [k];
return tSum [l-1] [m-1] [n-1];
C++
// C++ program for Min path sum of 3D-array#include<bits/stdc++.h>using namespace std;#define l 3#define m 3#define n 3 // A utility function that returns minimum// of 3 integersint min(int x, int y, int z){ return (x < y)? ((x < z)? x : z) : ((y < z)? y : z);} // function to calculate MIN path sum of 3D arrayint minPathSum(int arr[][m][n]){ int i, j, k; int tSum[l][m][n]; tSum[0][0][0] = arr[0][0][0]; /* Initialize first row of tSum array */ for (i = 1; i < l; i++) tSum[i][0][0] = tSum[i-1][0][0] + arr[i][0][0]; /* Initialize first column of tSum array */ for (j = 1; j < m; j++) tSum[0][j][0] = tSum[0][j-1][0] + arr[0][j][0]; /* Initialize first width of tSum array */ for (k = 1; k < n; k++) tSum[0][0][k] = tSum[0][0][k-1] + arr[0][0][k]; /* Initialize first row- First column of tSum array */ for (i = 1; i < l; i++) for (j = 1; j < m; j++) tSum[i][j][0] = min(tSum[i-1][j][0], tSum[i][j-1][0], INT_MAX) + arr[i][j][0]; /* Initialize first row- First width of tSum array */ for (i = 1; i < l; i++) for (k = 1; k < n; k++) tSum[i][0][k] = min(tSum[i-1][0][k], tSum[i][0][k-1], INT_MAX) + arr[i][0][k]; /* Initialize first width- First column of tSum array */ for (k = 1; k < n; k++) for (j = 1; j < m; j++) tSum[0][j][k] = min(tSum[0][j][k-1], tSum[0][j-1][k], INT_MAX) + arr[0][j][k]; /* Construct rest of the tSum array */ for (i = 1; i < l; i++) for (j = 1; j < m; j++) for (k = 1; k < n; k++) tSum[i][j][k] = min(tSum[i-1][j][k], tSum[i][j-1][k], tSum[i][j][k-1]) + arr[i][j][k]; return tSum[l-1][m-1][n-1]; } // Driver programint main(){ int arr[l][m][n] = { { {1, 2, 4}, {3, 4, 5}, {5, 2, 1}}, { {4, 8, 3}, {5, 2, 1}, {3, 4, 2}}, { {2, 4, 1}, {3, 1, 4}, {6, 3, 8}} }; cout << minPathSum(arr); return 0;} |
Java
// Java program for Min path sum of 3D-arrayimport java.io.*; class GFG { static int l =3; static int m =3; static int n =3; // A utility function that returns minimum // of 3 integers static int min(int x, int y, int z) { return (x < y)? ((x < z)? x : z) : ((y < z)? y : z); } // function to calculate MIN path sum of 3D array static int minPathSum(int arr[][][]) { int i, j, k; int tSum[][][] =new int[l][m][n]; tSum[0][0][0] = arr[0][0][0]; /* Initialize first row of tSum array */ for (i = 1; i < l; i++) tSum[i][0][0] = tSum[i-1][0][0] + arr[i][0][0]; /* Initialize first column of tSum array */ for (j = 1; j < m; j++) tSum[0][j][0] = tSum[0][j-1][0] + arr[0][j][0]; /* Initialize first width of tSum array */ for (k = 1; k < n; k++) tSum[0][0][k] = tSum[0][0][k-1] + arr[0][0][k]; /* Initialize first row- First column of tSum array */ for (i = 1; i < l; i++) for (j = 1; j < m; j++) tSum[i][j][0] = min(tSum[i-1][j][0], tSum[i][j-1][0], Integer.MAX_VALUE) + arr[i][j][0]; /* Initialize first row- First width of tSum array */ for (i = 1; i < l; i++) for (k = 1; k < n; k++) tSum[i][0][k] = min(tSum[i-1][0][k], tSum[i][0][k-1], Integer.MAX_VALUE) + arr[i][0][k]; /* Initialize first width- First column of tSum array */ for (k = 1; k < n; k++) for (j = 1; j < m; j++) tSum[0][j][k] = min(tSum[0][j][k-1], tSum[0][j-1][k], Integer.MAX_VALUE) + arr[0][j][k]; /* Construct rest of the tSum array */ for (i = 1; i < l; i++) for (j = 1; j < m; j++) for (k = 1; k < n; k++) tSum[i][j][k] = min(tSum[i-1][j][k], tSum[i][j-1][k], tSum[i][j][k-1]) + arr[i][j][k]; return tSum[l-1][m-1][n-1]; } // Driver program public static void main (String[] args) { int arr[][][] = { { {1, 2, 4}, {3, 4, 5}, {5, 2, 1}}, { {4, 8, 3}, {5, 2, 1}, {3, 4, 2}}, { {2, 4, 1}, {3, 1, 4}, {6, 3, 8}} }; System.out.println ( minPathSum(arr)); }} // This code is contributed by vt_m |
C#
// C# program for Min // path sum of 3D-arrayusing System; class GFG{ static int l = 3; static int m = 3; static int n = 3; // A utility function // that returns minimum // of 3 integers static int min(int x, int y, int z) { return (x < y) ? ((x < z) ? x : z) : ((y < z) ? y : z); } // function to calculate MIN // path sum of 3D array static int minPathSum(int [,,]arr) { int i, j, k; int [ , , ]tSum = new int[l, m, n]; tSum[0, 0, 0] = arr[0, 0, 0]; /* Initialize first row of tSum array */ for (i = 1; i < l; i++) tSum[i, 0, 0] = tSum[i - 1, 0, 0] + arr[i, 0, 0]; /* Initialize first column of tSum array */ for (j = 1; j < m; j++) tSum[0, j, 0] = tSum[0, j - 1, 0] + arr[0, j, 0]; /* Initialize first width of tSum array */ for (k = 1; k < n; k++) tSum[0, 0, k] = tSum[0, 0, k - 1] + arr[0, 0, k]; /* Initialize first row- First column of tSum array */ for (i = 1; i < l; i++) for (j = 1; j < m; j++) tSum[i, j, 0] = min(tSum[i - 1, j, 0], tSum[i, j - 1, 0], int.MaxValue) + arr[i, j, 0]; /* Initialize first row- First width of tSum array */ for (i = 1; i < l; i++) for (k = 1; k < n; k++) tSum[i, 0, k] = min(tSum[i - 1, 0, k], tSum[i, 0, k - 1], int.MaxValue) + arr[i, 0, k]; /* Initialize first width- First column of tSum array */ for (k = 1; k < n; k++) for (j = 1; j < m; j++) tSum[0, j, k] = min(tSum[0, j, k - 1], tSum[0, j - 1, k], int.MaxValue) + arr[0, j, k]; /* Construct rest of the tSum array */ for (i = 1; i < l; i++) for (j = 1; j < m; j++) for (k = 1; k < n; k++) tSum[i, j, k] = min(tSum[i - 1, j, k], tSum[i, j - 1, k], tSum[i, j, k - 1]) + arr[i, j, k]; return tSum[l-1,m-1,n-1]; } // Driver Code static public void Main () { int [, , ]arr= {{{1, 2, 4}, {3, 4, 5}, {5, 2, 1}}, {{4, 8, 3}, {5, 2, 1}, {3, 4, 2}}, {{2, 4, 1}, {3, 1, 4}, {6, 3, 8}}}; Console.WriteLine(minPathSum(arr)); }} // This code is contri
РЕКОМЕНДУЕМЫЕ СТАТЬИ |