Минимаксный алгоритм в теории игр | Набор 4 (альфа-бета-обрезка)
Предпосылки: минимаксный алгоритм в теории игр, оценочная функция в теории игр.
Альфа-бета-обрезка на самом деле не новый алгоритм, а метод оптимизации для минимаксного алгоритма. Это значительно сокращает время вычислений. Это позволяет нам искать намного быстрее и даже углубляться в уровни в дереве игры. Он отсекает ветви в дереве игры, в которых нет необходимости искать, потому что уже существует лучший ход. Это называется альфа-бета-обрезкой, потому что в минимаксной функции передаются два дополнительных параметра, а именно альфа и бета.
Определим параметры альфа и бета.
Альфа - это лучшее значение, которое в настоящее время может гарантировать максимайзер на этом уровне или выше.
Бета - это лучшее значение, которое минимизатор в настоящее время может гарантировать на этом уровне или выше.
Псевдокод:
функция минимакс (узел, глубина, isMaximizingPlayer, альфа, бета):
если узел является листовым узлом:
возвращаемое значение узла
если isMaximizingPlayer:
bestVal = -INFINITY
для каждого дочернего узла:
значение = минимакс (узел, глубина + 1, ложь, альфа, бета)
bestVal = max (bestVal, значение)
альфа = макс (альфа, bestVal)
если бета <= альфа:
перерыв
вернуть bestVal
еще :
bestVal = + БЕСКОНЕЧНОСТЬ
для каждого дочернего узла:
значение = минимакс (узел, глубина + 1, истина, альфа, бета)
bestVal = min (bestVal, значение)
beta = min (beta, bestVal)
если бета <= альфа:
перерыв
вернуть bestVal
// Вызов функции в первый раз. минимакс (0, 0, истина, -БЕСКОНЕЧНОСТЬ, + БЕСКОНЕЧНОСТЬ)
Поясним приведенный выше алгоритм на примере.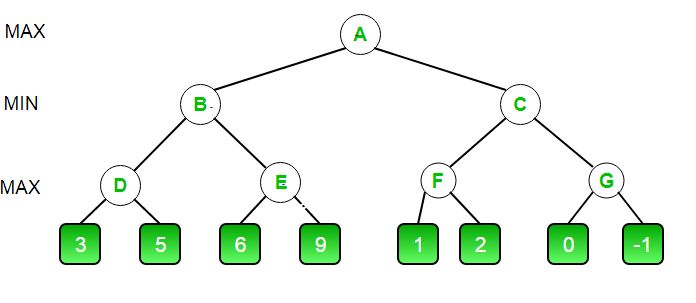
- Первоначальный вызов начинается с A. Значение альфы здесь -INFINITY, а значение beta + INFINITY . Эти значения передаются последующим узлам дерева. В точке A максимайзер должен выбрать максимум B и C , поэтому A сначала вызывает B.
- В точке B минимизатор должен выбрать min из D и E и, следовательно, сначала вызывает D.
- В D он смотрит на своего левого дочернего элемента, который является листовым узлом. Этот узел возвращает значение 3. Теперь значение альфа в D равно max (-INF, 3), что равно 3.
- Чтобы решить, стоит ли смотреть на правый узел или нет, он проверяет условие beta <= alpha. Это неверно, поскольку бета = + INF и альфа = 3. Итак, поиск продолжается.
- D теперь смотрит на своего правого дочернего элемента, который возвращает значение 5. В D alpha = max (3, 5), что равно 5. Теперь значение узла D равно 5.
- D возвращает значение 5 в B. В B бета = min (+ INF, 5), что равно 5. Минимизатору теперь гарантировано значение 5 или меньше. Теперь B вызывает E, чтобы узнать, может ли он получить значение ниже 5.
- В E значения альфа и бета не -INF и + INF, а вместо -INF и 5 соответственно, потому что значение бета было изменено в B, и это то, что B передало E
- Теперь E смотрит на своего левого дочернего элемента, который равен 6. В E , alpha = max (-INF, 6), который равен 6. Здесь условие становится истинным. бета равна 5, а альфа - 6. Так что бета <= альфа верно. Следовательно, он прерывается, и E возвращает 6 в B
- Обратите внимание на то, что значение правого дочернего элемента E не имело значения. Это могло быть + INF или -INF, это все равно не имело бы значения. Нам даже не пришлось на это смотреть, потому что минимизатору гарантировалось значение 5 или меньше. Итак, как только максимайзер увидел 6, он понял, что минимайзер никогда не пойдет по этому пути, потому что он может получить 5 слева от B. Таким образом, нам не нужно смотреть на эти 9 и, следовательно, сэкономить время вычислений.
- E возвращает значение 6 для B. В точке B beta = min (5, 6), что равно 5. Значение узла B также равно 5.
Так выглядит наше игровое дерево. Число 9 зачеркнуто, потому что оно никогда не вычислялось.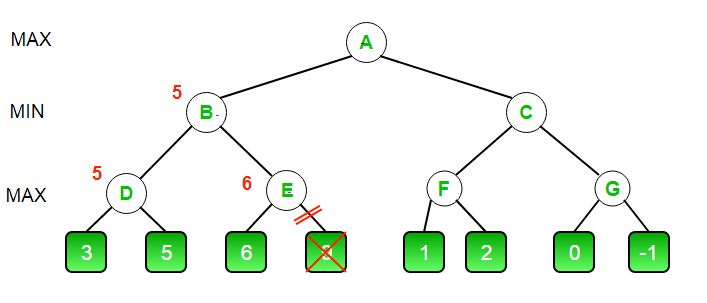
- B возвращает 5 к A. В A альфа = max (-INF, 5), что равно 5. Теперь максимизатору гарантировано значение 5 или больше. Теперь A вызывает C, чтобы узнать, может ли он получить значение выше 5.
- В C альфа = 5 и бета = + INF. C называет F
- В F альфа = 5 и бета = + INF. F смотрит на своего левого дочернего элемента, равного 1. alpha = max (5, 1), который по-прежнему равен 5.
- F смотрит на свой правый дочерний элемент, равный 2. Следовательно, лучшее значение этого узла равно 2. Альфа по-прежнему остается равной 5.
- F возвращает значение 2 в C. В C бета = min (+ INF, 2). Условие beta <= alpha становится истинным, если beta = 2 и alpha = 5. Таким образом, оно нарушается, и ему даже не нужно вычислять все поддерево G.
- Интуиция, стоящая за этим разрывом, заключается в том, что в C минимизатору гарантировалось значение 2 или меньше. Но максимайзеру уже гарантировано значение 5, если он выберет B. Так почему же максимайзер выбрал C и получил значение меньше 2? Опять же, вы можете видеть, что не имело значения, какими были эти последние 2 значения. Мы также сэкономили много вычислений, пропустив целое поддерево.
- Теперь C возвращает значение 2 для A. Следовательно, наилучшее значение для A - max (5, 2), что равно 5.
- Следовательно, оптимальное значение, которое может получить максимайзер, равно 5.
This is how our final game tree looks like. As you can see G has been crossed out as it was never computed.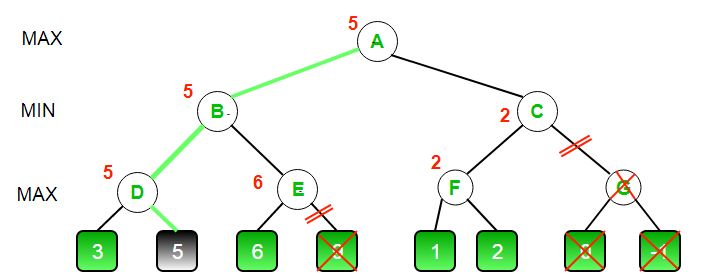
CPP
// C++ program to demonstrate// working of Alpha-Beta Pruning#include<bits/stdc++.h>using namespace std; // Initial values of// Aplha and Betaconst int MAX = 1000;const int MIN = -1000; // Returns optimal value for// current player(Initially called// for root and maximizer)int minimax(int depth, int nodeIndex, bool maximizingPlayer, int values[], int alpha, int beta){ // Terminating condition. i.e // leaf node is reached if (depth == 3) return values[nodeIndex]; if (maximizingPlayer) { int best = MIN; // Recur for left and // right children for (int i = 0; i < 2; i++) { int val = minimax(depth + 1, nodeIndex * 2 + i, false, values, alpha, beta); best = max(best, val); alpha = max(alpha, best); // Alpha Beta Pruning if (beta <= alpha) break; } return best; } else { int best = MAX; // Recur for left and // right children for (int i = 0; i < 2; i++) { int val = minimax(depth + 1, nodeIndex * 2 + i, true, values, alpha, beta); best = min(best, val); beta = min(beta, best); // Alpha Beta Pruning if (beta <= alpha) break; } return best; }} // Driver Codeint main(){ int values[8] = { 3, 5, 6, 9, 1, 2, 0, -1 }; cout <<"The optimal value is : "<< minimax(0, 0, true, values, MIN, MAX);; return 0;} |
Java
// Java program to demonstrate// working of Alpha-Beta Pruningimport java.io.*; class GFG { // Initial values of // Aplha and Betastatic int MAX = 1000;static int MIN = -1000; // Returns optimal value for// current player (Initially called// for root and maximizer)static int minimax(int depth, int nodeIndex, Boolean maximizingPlayer, int values[], int alpha, int beta){ // Terminating condition. i.e // leaf node is reached if (depth == 3) return values[nodeIndex]; if (maximizingPlayer) { int best = MIN; // Recur for left and // right children for (int i = 0; i < 2; i++) { int val = minimax(depth + 1, nodeIndex * 2 + i, false, values, alpha, beta); best = Math.max(best, val); alpha = Math.max(alpha, best); // Alpha Beta Pruning if (beta <= alpha) break; } return best; } else { int best = MAX; // Recur for left and // right children for (int i = 0; i < 2; i++) { int val = minimax(depth + 1, nodeIndex * 2 + i, true, values, alpha, beta); best = Math.min(best, val); beta = Math.min(beta, best); // Alpha Beta Pruning if (beta <= alpha) break; } return best; }} // Driver Code public static void main (String[] args) { int values[] = {3, 5, 6, 9, 1, 2, 0, -1}; System.out.println("The optimal value is : " + minimax(0, 0, true, values, MIN, MAX)); }} // This code is contributed by vt_m. |
Python3
# Python3 program to demonstrate # working of Alpha-Beta Pruning # Initial values of Aplha and Beta MAX, MIN = 1000, -1000 # Returns optimal value for current player #(Initially called for root and maximizer) def minimax(depth, nodeIndex, maximizingPlayer, values, alpha, beta): # Terminating condition. i.e # leaf node is reached if depth == 3: return values[nodeIndex] if maximizingPlayer: best = MIN # Recur for left and right children for i in range(0, 2): val = minimax(depth + 1, nodeIndex * 2 + i, False, values, alpha, beta) best = max(best, val) alpha = max(alpha, best) # Alpha Beta Pruning if beta <= alpha: break return best else: best = MAX # Recur for left and # right children for i in range(0, 2): val = minimax(depth + 1, nodeIndex * 2 + i, True, values, alpha, beta) best = min(best, val) beta = min(beta, best) # Alpha Beta Pruning if beta <= alpha: break return best # Driver Code if __name__ == "__main__": values = [3, 5, 6, 9, 1, 2, 0, -1] print("The optimal value is :", minimax(0, 0, True, values, MIN, MAX)) # This code is contributed by Rituraj Jain |
C#
// C# program to demonstrate// working of Alpha-Beta Pruningusing System; class GFG { // Initial values of // Aplha and Betastatic int MAX = 1000;static int MIN = -1000; // Returns optimal value for// current player (Initially called// for root and maximizer)static int minimax(int depth, int nodeIndex, Boolean maximizingPlayer, int []values, int alpha, int beta){ // Terminating condition. i.e // leaf node is reached if (depth == 3) return values[nodeIndex]; if (maximizingPlayer) { int best = MIN; // Recur for left and // right children for (int i = 0; i < 2; i++) { int val = minimax(depth + 1, nodeIndex * 2 + i, false, values, alpha, beta); best = Math.Max(best, val); alpha = Math.Max(alpha, best); // Alpha Beta Pruning if (beta <= alpha) break; } return best; } else { int best = MAX; // Recur for left and // right children for (int i = 0; i < 2; i++) { int val = minimax(depth + 1, nodeIndex * 2 + i, true, values, alpha, beta); best = Math.Min(best, val); beta = Math.Min(beta, best); // Alpha Beta Pruning if (beta <= alpha) break; } return best; }} // Driver Codepublic static void Main (String[] args){ int []values = {3, 5, 6, 9, 1, 2, 0, -1}; Console.WriteLine("The optimal value is : " + minimax(0, 0, true, values, MIN, MAX)); }} // This code is contributed by 29AjayKumar |
Output :
The optimal value is : 5
Автор статьи - Акшай Л Арадхья. Если вам нравится GeeksforGeeks, и вы хотели бы внести свой вклад, вы также можете написать статью на сайте deposit.geeksforgeeks.org или отправить свою статью по электронной почте: grant@geeksforgeeks.org. Посмотрите, как ваша статья появляется на главной странице GeeksforGeeks, и помогите другим гикам.
Пожалуйста, напишите комментарии, если вы обнаружите что-то неправильное, или вы хотите поделиться дополнительной инф