Математика | Замыкание отношений и отношения эквивалентности
Предпосылки: Введение в отношения, представление отношений
Объединение отношений:
Поскольку мы знаем, что отношения - это просто наборы упорядоченных пар, поэтому все операции над наборами применимы и к ним. Два отношения можно комбинировать несколькими способами, например:
- Союз -
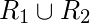 состоит из всех упорядоченных пар из обоих отношений. Повторяющиеся упорядоченные пары удалены из Union.
состоит из всех упорядоченных пар из обоих отношений. Повторяющиеся упорядоченные пары удалены из Union. - Пересечение -
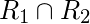 состоит из упорядоченных пар, находящихся в обоих отношениях.
состоит из упорядоченных пар, находящихся в обоих отношениях. - Разница -
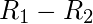 состоит из всех упорядоченных пар только в
состоит из всех упорядоченных пар только в 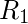 , но не в
, но не в 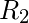 .
. - Симметричная разница -
 состоит из всех упорядоченных пар, находящихся либо в
состоит из всех упорядоченных пар, находящихся либо в 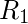 или
или 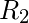 но не то и другое одновременно.
но не то и другое одновременно.
Есть еще один способ объединения двух отношений, аналогичный композиции функций.
Композиция - Пусть  быть родственником из
быть родственником из 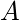 к
к 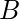 а также
а также 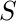 быть родственником из
быть родственником из 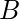 к
к 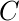 , то композиция
, то композиция  а также
а также 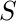 , обозначаемый
, обозначаемый 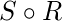 , - отношение, состоящее из упорядоченных пар
, - отношение, состоящее из упорядоченных пар 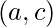 куда
куда 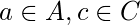 и для которого существует элемент
и для которого существует элемент 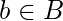 такой, что
такой, что 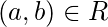 а также
а также 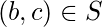 .
.
- Пример - Какова композиция отношений
 а также
а также 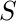 куда
куда  это отношение из
это отношение из 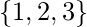 к
к 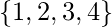 с участием
с участием 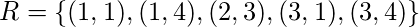 а также
а также 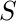 это отношение из
это отношение из 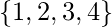 к
к 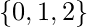 с участием
с участием 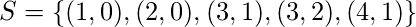 ?
? - Решение - вычисляя все упорядоченные пары, в которых первый элемент принадлежит
 а второй элемент принадлежит
а второй элемент принадлежит 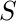 , мы получаем -
, мы получаем - 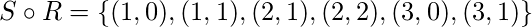
Состав отношения к себе:
Отношение может быть составлено с самим собой, чтобы получить степень разделения между элементами множества, на котором  определено.
определено.
Позволятьотношение на множестве
. Полномочия
куда
определяются рекурсивно:
а также
.
Теорема - Пусть  - отношение на множестве A, представленное ди-графом. Есть путь длины
- отношение на множестве A, представленное ди-графом. Есть путь длины 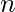 , куда
, куда 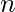 положительное целое число, от
положительное целое число, от 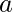 к
к 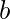 если и только если
если и только если 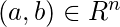 .
.
Важное примечание: отношение  на съемочной площадке
на съемочной площадке 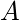 транзитивен тогда и только тогда, когда
транзитивен тогда и только тогда, когда 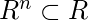 для
для 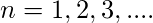
Завершение отношений:
Рассмотрим отношение  на съемочной площадке
на съемочной площадке 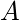 .
.  может иметь или не иметь собственность
может иметь или не иметь собственность 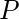 , например рефлексивность, симметрия или транзитивность.
, например рефлексивность, симметрия или транзитивность.
Если есть отношение 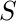 с собственностью
с собственностью 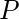 содержащий
содержащий  такой, что
такой, что 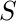 это подмножество
это подмножество
всякого отношения к собственности 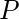 содержащий
содержащий  , тогда
, тогда 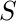 называется закрытием
называется закрытием  относительно
относительно 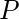 .
.
Мы можем получить замыкания отношений по свойству 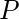 следующими способами -
следующими способами -
- Рефлексивное закрытие -
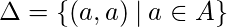 диагональное отношение на множестве
диагональное отношение на множестве 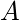 . Рефлексивное завершение отношения
. Рефлексивное завершение отношения  на съемочной площадке
на съемочной площадке 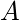 является
является 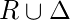 .
. - Симметричное замыкание - Пусть
 быть отношением на множестве
быть отношением на множестве 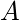 , и разреши
, и разреши 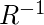 быть инверсией
быть инверсией  . Симметричное замыкание отношения
. Симметричное замыкание отношения  на съемочной площадке
на съемочной площадке 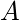 является
является 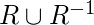 .
. - Переходное замыкание - Пусть
 быть отношением на множестве
быть отношением на множестве 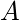 . Отношение связности определяется как -
. Отношение связности определяется как - 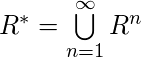 . Переходное замыкание
. Переходное замыкание  является
является 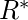 .
.
Пример - Пусть  быть отношением на множестве
быть отношением на множестве 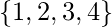 с участием
с участием 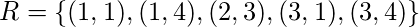 . Найдите рефлексивное, симметричное и транзитивное замыкание R.
. Найдите рефлексивное, симметричное и транзитивное замыкание R.
Решение -
Для данного набора 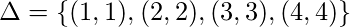 . Итак, рефлексивное закрытие
. Итак, рефлексивное закрытие  является
является 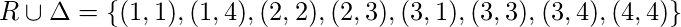
Для симметричного замыкания нам понадобится обратное к  , который
, который 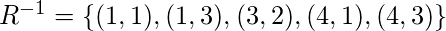 .
.
Симметричное замыкание  является-
является- 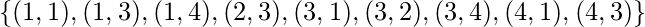
Для транзитивного замыкания нам нужно найти 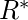 .
.  нам нужно найти
нам нужно найти 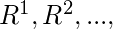 до
до 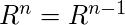 . Мы останавливаемся, когда это условие достигнуто, так как находим более высокие степени
. Мы останавливаемся, когда это условие достигнуто, так как находим более высокие степени  будет то же самое.
будет то же самое. 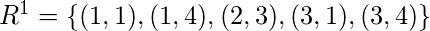
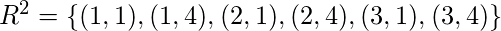
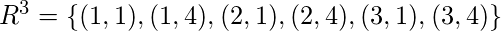
С, 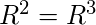 мы останавливаем процесс.
мы останавливаем процесс.
Переходное закрытие, 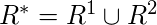 -
- 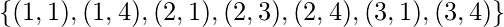
Отношения эквивалентности:
Позволять  быть отношением на множестве
быть отношением на множестве 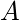 . Если
. Если  рефлексивно, симметрично и транзитивно, то называется отношением эквивалентности.
рефлексивно, симметрично и транзитивно, то называется отношением эквивалентности.
Следовательно, два элемента 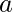 а также
а также 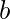 связанные отношением эквивалентности, называются эквивалентными.
связанные отношением эквивалентности, называются эквивалентными.
Пример - Покажите, что отношение 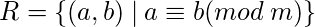 является отношением эквивалентности.
является отношением эквивалентности. 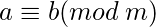 сравнение по модулю
сравнение по модулю 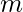 функция. Это верно тогда и только тогда, когда
функция. Это верно тогда и только тогда, когда 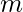 разделяет
разделяет  .
.
Решение. Чтобы показать, что отношение является отношением эквивалентности, мы должны доказать, что отношение рефлексивно, симметрично и транзитивно.
- Reflexive - для любого элемента
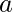 ,
, 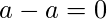 делится на
делится на 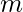 .
. 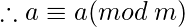 . Итак, сравнение по модулю
. Итак, сравнение по модулю 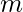 рефлексивно.
рефлексивно. - Симметричный - для любых двух элементов
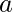 а также
а также 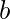 , если
, если 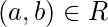 или
или 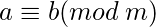 т.е.
т.е.  делится на
делится на 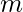 , тогда
, тогда 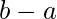 также делится на
также делится на 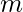 .
. 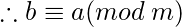 . Так что по модулю сравнения
. Так что по модулю сравнения 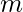 симметрично.
симметрично. - Переходный - для любых трех элементов
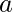 ,
, 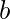 , а также
, а также 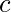 если
если 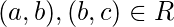 тогда-
тогда- 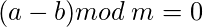
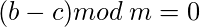
Сложив оба уравнения,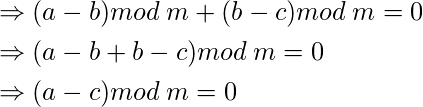
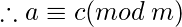 . Так,
. Так,  транзитивен.
транзитивен.Поскольку отношение
 рефлексивно, симметрично и транзитивно, заключаем, что
рефлексивно, симметрично и транзитивно, заключаем, что  является отношением эквивалентности.
является отношением эквивалентности.Классы эквивалентности:
Позволять
 - отношение эквивалентности на множестве
- отношение эквивалентности на множестве 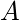 .
.
Мы знаем, что если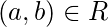 тогда
тогда 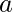 а также
а также 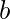 называются эквивалентными относительно
называются эквивалентными относительно  .
.Набор всех элементов, связанных с элементом
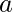 из
из 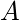 называется
называется
класс эквивалентности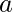 . Обозначается он
. Обозначается он 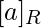 или просто
или просто 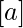 если есть только один
если есть только один
отношение к рассмотрению.
Формально,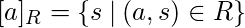
Любой элемент
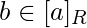 считается представителем
считается представителем 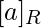 .
.
Важное примечание: все классы эквивалентности отношения на съемочной площадке
на съемочной площадке 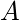 либо равны, либо не пересекаются, и их объединение дает множество
либо равны, либо не пересекаются, и их объединение дает множество 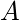 .
. 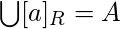
Классы эквивалентности также называются разбиениями, поскольку они не пересекаются, и их объединение дает набор, на котором определено отношение.- Пример: каковы классы эквивалентности отношения Congruence Modulo
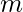 ?
? - Решение: пусть
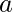 а также
а также 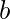 быть двумя числами такими, что
быть двумя числами такими, что 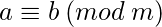 . Это означает, что остаток, полученный от деления
. Это означает, что остаток, полученный от деления 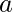 а также
а также 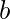 с участием
с участием 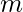 та же.
та же.
Возможные значения остатка -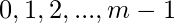
Следовательно, есть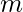 классы эквивалентности -
классы эквивалентности - 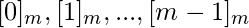
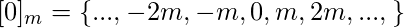
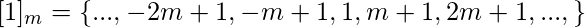


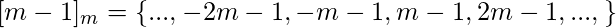
Вопросы по GATE CS Corner
Выполнение следующих вопросов поможет вам проверить свои знания. Все вопросы задавались в GATE в предыдущие годы или в пробных тестах GATE. Настоятельно рекомендуется попрактиковаться в них.
1. GATE CS 2013, вопрос 1
2. GATE CS 2005, вопрос 42
3. GATE CS 2001, вопрос 2
4. GATE CS 2000, вопрос 28Использованная литература -
Состав отношений - Википедия
Дискретная математика и ее приложения, Кеннет Х. РозенЭта статья предоставлена Чирагом Манвани . Если вам нравится GeeksforGeeks, и вы хотели бы внести свой вклад, вы также можете написать статью с помощью provide.geeksforgeeks.org или отправить ее по электронной почте на deposit@geeksforgeeks.org. Посмотрите, как ваша статья появляется на главной странице GeeksforGeeks, и помогите другим гикам.
Пожалуйста, напишите комментарии, если вы обнаружите что-то неправильное, или вы хотите поделиться дополнительной информацией по теме, обсужденной выше.
- Пример: каковы классы эквивалентности отношения Congruence Modulo