Математика | Сумма квадратов четных и нечетных натуральных чисел

Мы знаем, что сумма квадратов первых n натуральных чисел равна .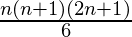

Как вычислить сумму квадратов первых n четных натуральных чисел?
Нам нужно вычислить 2 ² + 4 ² + 6 ² +…. + (2n) ²

EvenSum = 2 2 + 4 2 + 6 2 + .... + (2n) 2 
        = 4 х (1 2 + 2 2 + 3 2 + .... + (n) 2 )
        = 4n (n + 1) (2n + 1) / 6
        = 2n (n + 1) (2n + 1) / 3

Пример:

 Сумма квадратов первых трех четных чисел =
                 2n (n + 1) (2n + 1) / 3
               = 2 * 3 (3 + 1) (2 * 3 + 1) / 3
               = 56
22 + 42 + 62 = 4 + 16 + 36 = 56

Как вычислить сумму квадратов первых n нечетных натуральных чисел?
Нам нужно вычислить 1 ² + 3 ² + 5 ² +…. + (2н-1) ²

OddSum = (сумма квадратов всех 2n чисел) - 
          (Сумма квадратов первых n четных чисел)
        = 2n * (2n + 1) * (2 * 2n + 1) / 6 - 2n (n + 1) (2n + 1) / 3
        = 2n (2n + 1) / 6 [4n + 1-2 (n + 1)] 
        = п (2n + 1) / 3 * (2n-1)
        = п (2n + 1) (2n-1) / 3

Пример:

Сумма квадратов первых 3 нечетных чисел = n (2n + 1) (2n-1) / 3
                                      = 3 (2 * 3 + 1) (2 * 3-1) / 3
                                      = 35
1 2 + 3 2 + 5 2 = 1 + 9 + 25 = 35

Пожалуйста, напишите комментарии, если вы обнаружите что-то неправильное, или вы хотите поделиться дополнительной информацией по теме, обсужденной выше